Physics engine - Part 1: Ball collisions
In this part, we'll set up a crate for our physics engine, implement the core simulation loop and get some balls to collide.
Setting up the bevy project
Make a new rust library
cargo new --lib bevy_xpbd
And add bevy as a dependency in Cargo.toml:
[dependencies]
bevy = "0.6"
We will be testing most of our development in example applications. Create a new example by making an examples folder and a new file simple.rs within it:
use bevy::prelude::*;
use bevy_xpbd::*;
fn main() {
App::new()
.insert_resource(ClearColor(Color::BLACK))
.insert_resource(Msaa { samples: 4 })
.add_plugins(DefaultPlugins)
.run();
}
You should now be able to start our empty example by running:
cargo run --example simple
Or if you have cargo-watch installed (which I highly recommend) run this to rebuild and re-run the example each time you save:
cargo watch -cx -- "run --example simple"
Without all the boring boiler-plate out of the way, we can now focus on actually building the physics engine.
Representation of objects
We will be making a 2D physics engine using a variant of position-based dynamics. So unsurprisingly the most central component will be positions.
One option would have been to use the translation field on Bevy's Transform component, however there are two reasons not to do this:
- We are making a 2D simulation, and we only really need x and y positions, while Transform has fields for z-position, scale and rotation, and it's nice not to waste memory or get more cache misses.
- There could be different ways to update the displayed position (interpolation/extrapolation etc.) so it might be convenient to keep it separate.
We will be using a newtype of Vec2 to represent objects' positions. In lib.rs, delete the example code generated by cargo new and create a new Pos type:
use bevy::prelude::*;
#[derive(Component, Debug, Default)]
pub struct Pos(pub Vec2);
Now lets head back to our example, and add a sprite with a Pos component.
Create a new startup system:
fn startup(
mut commands: Commands,
mut meshes: ResMut<Assets<Mesh>>,
mut materials: ResMut<Assets<StandardMaterial>>,
) {
let sphere = meshes.add(Mesh::from(shape::Icosphere {
radius: 0.5,
subdivisions: 4,
}));
let white = materials.add(StandardMaterial {
base_color: Color::WHITE,
unlit: true,
..Default::default()
});
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert(Pos(Vec2::ZERO));
commands.spawn_bundle(OrthographicCameraBundle {
transform: Transform::from_translation(Vec3::new(0., 0., 100.)),
orthographic_projection: bevy::render::camera::OrthographicProjection {
scale: 0.01,
..Default::default()
},
..OrthographicCameraBundle::new_3d()
});
}
And register it in main:
App::new()
.insert_resource(ClearColor(Color::BLACK))
.insert_resource(Msaa { samples: 4 })
.add_plugins(DefaultPlugins)
.add_startup_system(startup)
.run();
If you now start the example, you should see a black window with a white circle in the middle.
We will be starting off with circles/particles as that makes most of the math really simple, and then we will extend to more complex shapes once we have the basic simulation going.

Making things move
Alright, lets move on to implement the basics of position-based dynamics.
Lets say we want the particle on the screen to start with an initial velocity of 2 units to the right, so it should move 2 units each second.
In position-based dynamics, velocities are not really first-class citizens, they are derived based on the current and the last frame's positions. That is:
velocity = (v_current - v_previous) / delta_time
So in order to initialize our particle with a "velocity", what we really need to do, is compute and a corresponding previous position. Reordering the above equation, we get:
v_previous = v_current - velocity * delta_time
Converting this into rust code, we get:
// Spawn circle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert(PrevPos(Vec2::ZERO - Vec2::new(2., 0.) * DELTA_TIME))
.insert(Pos(Vec2::ZERO));
In order for this to work, we need to add two things in lib.rs:
The PrevPos component, another Vec2 newtype:
#[derive(Component, Debug, Default)]
pub struct PrevPos(pub Vec2);
And the DELTA_TIME constant:
pub const DELTA_TIME: f32 = 1. / 60.;
We will revisit DELTA_TIME later and make it configurable when we add sub-stepping, but for now we just leave it at 60 FPS.
We now have the necessary data set up, and we just need to add systems that operate on these values to actually move the object.
Lets create two new systems in lib.rs:
/// Moves objects in the physics world
pub fn simulate(mut query: Query<(&mut Pos, &mut PrevPos)>) {
for (mut pos, mut prev_pos) in query.iter_mut() {
let velocity = (pos.0 - prev_pos.0) / DELTA_TIME;
prev_pos.0 = pos.0;
pos.0 = pos.0 + velocity * DELTA_TIME;
}
}
/// Copies positions from the physics world to bevy Transforms
pub fn sync_transforms(mut query: Query<(&mut bevy::transform::components::Transform, &Pos)>) {
for (mut transform, pos) in query.iter_mut() {
transform.translation = pos.0.extend(0.);
}
}
Now add these two systems to the example:
.add_startup_system(startup)
.add_system(simulate) // <--
.add_system(sync_transforms) // <--
.run();
Your circle should now slowly slide off the screen.
What we've now implemented in simulate() is what's often called the integrator.
Keeping things neat
Now is a good time to take a step back and take a look at the structure of our code. The first thing that really screams leaking of implementation details, is the two lines we just added to the example. We don't want to require our users to update their code every time we decide to add, remove or rename a system. We fix this by bundling the systems in a plugin:
// lib.rs
#[derive(Debug, Default)]
pub struct XPBDPlugin;
impl Plugin for XPBDPlugin {
fn build(&self, app: &mut App) {
app.add_system(simulate)
.add_system(sync_transforms);
}
}
And in the example, we can now remove the two systems and add the plugin instead:
fn main() {
App::new()
.insert_resource(ClearColor(Color::BLACK))
.insert_resource(Msaa { samples: 4 })
.add_plugins(DefaultPlugins)
.add_plugin(XPBDPlugin::default()) // <-- new
.add_startup_system(startup)
.run();
}
For good measure, let's also make the systems private:
// lib.rs
fn simulate(mut query: Query<(&mut Pos, &mut PrevPos)>) {
// ...
}
fn sync_transforms(mut query: Query<(&mut bevy::transform::components::Transform, &Pos)>) {
// ...
}
The other thing that really stands out, is the computation of PrevPos.
We can make this a little bit better by providing a ParticleBundle that contains both a Pos and a PrevPos. In a new file src/entity.rs
use bevy::prelude::*;
use crate::*;
#[derive(Bundle, Default)]
pub struct ParticleBundle {
pub pos: Pos,
pub prev_pos: PrevPos,
}
impl ParticleBundle {
pub fn new_with_pos_and_vel(pos: Vec2, vel: Vec2) -> Self {
Self {
pos: Pos(pos),
prev_pos: PrevPos(pos - vel * DELTA_TIME),
}
}
}
Then add the new module in lib.rs
mod entity;
pub use entity::*;
And finally, we can get rid of DELTA_TIME and PrevPos in simple.rs:
// Spawn circle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert_bundle(ParticleBundle::new_with_pos_and_vel(
Vec2::ZERO,
Vec2::new(2., 0.),
));
This is enough for now, let's get on with the simulation.
Fixing the broken time step
Now, if you paid close attention, you might have noticed that we hard-coded DELTA_TIME to be 16 ms (60 FPS), but we are running the simulation in a regular system (app.add_system). The problem with this, is that the simulation speed now depends on the frame rate.
Let's fix this by making sure our systems are actually run at the specified DELTA_TIME
// lib.rs
use bevy::{core::FixedTimestep, prelude::*};
// ...
#[derive(Debug, Hash, PartialEq, Eq, Clone, StageLabel)]
struct FixedUpdateStage;
// ...
impl Plugin for XPBDPlugin {
fn build(&self, app: &mut App) {
app.add_stage_before(
CoreStage::Update,
FixedUpdateStage,
SystemStage::parallel()
.with_run_criteria(FixedTimestep::step(DELTA_TIME as f64))
.with_system(simulate)
.with_system(sync_transforms),
);
}
}
Now we can start to see how keeping the system setup encapsulated in a plugin starts to pay off.
Adding gravity
Ok, I know I promised interactions and fluids and everything, and so far all we have is a sliding circle. It's time to make something a little bit more exciting. So let's add gravity!
Gravity is what's known as an "external force", in PBD, these forces are converted and added directly to the computed velocity immediately before we update the new position.
In order to get an actual gravitation force and not just an acceleration, we need our particles to have mass, so we should add a new Mass component. Our lib.rs file is getting a little bit untidy, though, so lets move PrevPos and Pos to a new module, components.rs and then add the new component there.
use bevy::prelude::*;
#[derive(Component, Debug, Default)]
pub struct Pos(pub Vec2);
#[derive(Component, Debug, Default)]
pub struct PrevPos(pub Vec2);
#[derive(Component, Debug)]
pub struct Mass(pub f32);
impl Default for Mass {
fn default() -> Self {
Self(1.) // Default to 1 kg
}
}
Then add the new module to our list of modules:
// lib.rs
mod components;
mod entity;
pub use components::*;
pub use entity::*;
Ok, so we have a mass component, but we need to make sure it's actually added to our particles as well:
// entity.rs
pub struct ParticleBundle {
pub pos: Pos,
pub prev_pos: PrevPos,
pub mass: Mass, // <-- new
}
impl ParticleBundle {
pub fn new_with_pos_and_vel(pos: Vec2, vel: Vec2) -> Self {
Self {
pos: Pos(pos),
prev_pos: PrevPos(pos - vel * DELTA_TIME),
..Default::default(), // <-- new
}
}
}
Now we're finally ready to add mass and gravity to our simulate system:
fn simulate(mut query: Query<(&mut Pos, &mut PrevPos, &Mass)>) {
for (mut pos, mut prev_pos, mass) in query.iter_mut() {
let gravity = Vec2::new(0., -9.81);
let gravitation_force = mass.0 * gravity;
let external_forces = gravitation_force;
let velocity = (pos.0 - prev_pos.0) / DELTA_TIME + DELTA_TIME * external_forces / mass.0;
// ...
}
}
Now, you may have spotted that this could actually be simplified by removing the mass (as we first multiply by it, then divide by it), but we will keep it like this as it will make it easier for us later.
If you run the example now, you should see the particle falling down.
Configuration
Now let's take a moment again to look at the code. So we added gravity to the simulation, which is cool, but it's pretty inflexible as it's hard-coded to -9.81f. What if we want a space simulation or top-down simulation like a pool game?
We can make the gravity configurable by putting it in a bevy resource.
// lib.rs
fn build(&self, app: &mut App) {
app.init_resource::<Gravity>()
// ...
}
// ...
#[derive(Debug)]
pub struct Gravity(pub Vec2);
impl Default for Gravity {
fn default() -> Self {
Self(Vec2::new(0., -9.81))
}
}
// ...
fn simulate(mut query: Query<(&mut Pos, &mut PrevPos, &Mass)>, gravity: Res<Gravity>) {
for (mut pos, mut prev_pos, mass) in query.iter_mut() {
let gravitation_force = mass.0 * gravity.0;
let external_forces = gravitation_force;
The example should run as before since we default to earth gravity. Lets create a new example to test with no gravity.
Copy simple.rs into a new file particle_collisions.rs (we will use this to set up a new example in the next section). And set the gravity in main:
.add_plugin(XPBDPlugin::default())
.insert_resource(Gravity(Vec2::ZERO)) // <-- new
.add_startup_system(startup)
If you now start this example it should run like it did before we added gravity.
Setting up a collision example
Ok, it's finally time to start making some collisions. We will update particle_collisions.rs and add another circle to it, moving the opposite way:
// Left particle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert_bundle(ParticleBundle::new_with_pos_and_vel(
Vec2::new(-2., 0.),
Vec2::new(2., 0.),
));
// Right particle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert_bundle(ParticleBundle::new_with_pos_and_vel(
Vec2::new(2., 0.),
Vec2::new(-2., 0.),
));
If you start the example now, you should see the two particles moving straight through each other. Let's fix that!
The first thing we need to figure out is how to detect if the particles collide. Right now, we haven't really thought much about the shape of objects. We are rendering a sphere, but nothing in the model actually defines the shape of our particles. Let's create a new component for that:
// components.rs
#[derive(Debug)]
pub struct CircleCollider {
pub radius: f32,
}
impl Default for CircleCollider {
fn default() -> Self {
Self { radius: 0.5 }
}
}
Let's also add it to ParticleBundle for now, we can worry about how to instantiate other shapes later.
// entity.rs
#[derive(Bundle, Default)]
pub struct ParticleBundle {
pub pos: Pos,
pub prev_pos: PrevPos,
pub mass: Mass,
pub collider: CircleCollider, // <-- new
}
Let's take a look at the definition of the XPBD rigid body simulation as defined in the paper I linked earlier and compare it to what we have so far:

There are a lot of ω's and q's. They are related to rotation, which we will ignore for now, that leaves us with:
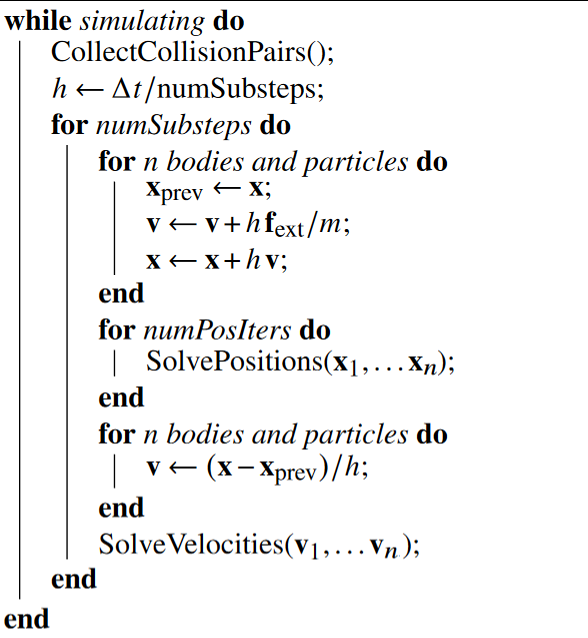
Compare this to what we have so far:
fn simulate(mut query: Query<(&mut Pos, &mut PrevPos, &Mass)>, gravity: Res<Gravity>) {
for (mut pos, mut prev_pos, mass) in query.iter_mut() {
let gravitation_force = mass.0 * gravity.0;
let external_forces = gravitation_force;
let velocity = (pos.0 - prev_pos.0) / DELTA_TIME + DELTA_TIME * external_forces / mass.0;
prev_pos.0 = pos.0;
pos.0 = pos.0 + velocity * DELTA_TIME;
}
}
They are kind of similar, but some things are different.
First, there is the CollectCollisionPairs step. We haven't added collisions yet, so we can ignore that for now.
Then there are the substeps, we will definitely add those, but let's ignore them for now (pretend numSubsteps = 1). We got more fundamental things to fix.
There are the SolvePositions and SolveVelocities steps which we don't have yet, which we will also add really soon.
So what we really have at this point, is this:
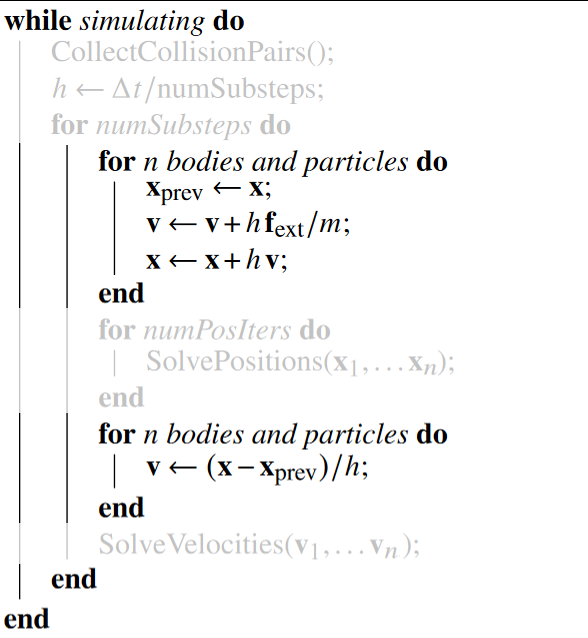
Now we can start moving things around to adapt to XPBD.
Comparing to our code, we see that XPBD has two loops, one that adds external forces and predicts the next position and velocity, and one that updates the velocities after the SolvePositions step. In our code, we've computed the velocity at the start of our single loop, while here it happens in between the two solve steps. We got away with this because we didn't have the SolvePositions step, so we could just merge the two loops and keep the velocity on the stack. However, we will be adding SolvePositions so let's adapt our code to fit the pseudo-code.
First, we need to add a new Vel component which will store the velocity
// components.rs
#[derive(Component, Debug, Default)]
pub struct Vel(pub(crate) Vec2);
// entity.rs
pub struct ParticleBundle {
pub pos: Pos,
pub prev_pos: PrevPos,
pub mass: Mass,
pub collider: CircleCollider,
pub vel: Vel, // <-- new
}
impl ParticleBundle {
pub fn new_with_pos_and_vel(pos: Vec2, vel: Vec2) -> Self {
Self {
pos: Pos(pos),
prev_pos: PrevPos(pos - vel * DELTA_TIME),
vel: Vel(vel), // <-- new
..Default::default()
}
}
}
Now, we can finally split our simulate loop into two loops and do the velocity update in the same fashion as XPBD.
fn simulate(mut query: Query<(&mut Pos, &mut PrevPos, &mut Vel, &Mass)>, gravity: Res<Gravity>) {
// TODO: CollectCollisionPairs
for (mut pos, mut prev_pos, mut vel, mass) in query.iter_mut() {
prev_pos.0 = pos.0;
let gravitation_force = mass.0 * gravity.0;
let external_forces = gravitation_force;
vel.0 += DELTA_TIME * external_forces / mass.0;
pos.0 += DELTA_TIME * vel.0;
}
// TODO: SolvePositions
for (pos, prev_pos, mut vel, _mass) in query.iter_mut() {
vel.0 = (pos.0 - prev_pos.0) / DELTA_TIME;
}
// TODO: SolveVelocities
}
If you run the examples now, it should look exactly as before.
I left in todos in the code so it's easier to see where we are missing things compared to the XPBD pseudo-code definition.
Putting it into systems
Taking a look at our code from an ECS perspective again, it seems kind of clear that what we have could easily be split into two systems. We also have three todos. Let's implement placeholder systems for all of these as well and split our simulate system into five systems:
fn collect_collision_pairs() {}
fn integrate(mut query: Query<(&mut Pos, &mut PrevPos, &mut Vel, &Mass)>, gravity: Res<Gravity>) {
for (mut pos, mut prev_pos, mut vel, mass) in query.iter_mut() {
prev_pos.0 = pos.0;
let gravitation_force = mass.0 * gravity.0;
let external_forces = gravitation_force;
vel.0 += DELTA_TIME * external_forces / mass.0;
pos.0 += DELTA_TIME * vel.0;
}
}
fn solve_pos() {}
fn update_vel(mut query: Query<(&Pos, &PrevPos, &mut Vel)>) {
for (pos, prev_pos, mut vel) in query.iter_mut() {
vel.0 = (pos.0 - prev_pos.0) / DELTA_TIME;
}
}
fn solve_vel() {}
Notice also how we were able to remove Mass and relax the mutability constraints for velocity update query.
Heading back to our plugin code, we now need to make sure all of our systems run, so we add them instead of simulate
SystemStage::parallel()
.with_run_criteria(FixedTimestep::step(DELTA_TIME as f64))
.with_system(collect_collision_pairs)
.with_system(integrate)
.with_system(solve_pos)
.with_system(update_vel)
.with_system(solve_vel)
.with_system(sync_transforms),
However, we also need to ensure the systems are run in the right order.
To do this we will first add system labels for each of our new systems:
#[derive(SystemLabel, Debug, Hash, PartialEq, Eq, Clone)]
enum Step {
CollectCollisionPairs,
Integrate,
SolvePositions,
UpdateVelocities,
SolveVelocities,
}
Then we add the labels to the systems and add constraints as needed:
SystemStage::parallel()
.with_run_criteria(FixedTimestep::step(DELTA_TIME as f64))
.with_system(
collect_collision_pairs
.label(Step::CollectCollisionPairs)
.before(Step::Integrate),
)
.with_system(integrate.label(Step::Integrate))
.with_system(solve_pos.label(Step::SolvePositions).after(Step::Integrate))
.with_system(
update_vel
.label(Step::UpdateVelocities)
.after(Step::SolvePositions),
)
.with_system(
solve_vel
.label(Step::SolveVelocities)
.after(Step::UpdateVelocities),
)
.with_system(sync_transforms.after(Step::SolveVelocities)),
We also make sure sync_transforms is run after we've solved for velocities.
Once again, the examples should run as before, but our code is much more ECS-friendly now, and we can start implementing the various steps. Let's see how we can make these circles interact with each other, and implement the rest of the steps of the algorithm.
First we've got the CollectCollisionPairs step, this step is responsible for collecting potentially colliding bodies and store them in a list so they can be used in SolvePositions and SolveVelocities later. Since there is no harm (except for performance) to assume all possible combinations of bodies are potentially colliding, we will do that for now, and skip this step until we start optimizing. For now we just want to focus on getting a correct simulation with a minimal set of features.
Moving on to SolvePositions it gets more interesting. In XPBD (and PBD for that matter) the position solve step is where the magic happens. When objects are interacting in one way or the other, either through collisions or by being attached with a hinge, spring or distance joint (or if they are particles that are part of the same cloth or fluid), this step is what makes sure these rules are followed. That nothing gets in a "wrong position". These "rules" are collectively referred to as "constraints". Collisions are handled using "non-penetration" constraints, while hinges, springs and fixed distances are referred to as "joint constraints".
Implementing a non-penetration constraint
So looking at our example, and what's wrong with it, our intuition tells us that the two circles should not be overlapping, so let's fix it by implementing a non-penetration constraint for our circles.
First, we need a way to iterate over all pairs of bodies.
The simplest way to do this, is using .iter_combinations_mut(). It returns all possible pairs without repeating.
fn solve_pos(mut query: Query<(&mut Pos, &CircleCollider)>) {
let mut iter = query.iter_combinations_mut();
while let Some([(mut pos_a, circle_a), (mut pos_b, circle_b)]) =
iter.fetch_next()
{
let ab = pos_b.0 - pos_a.0;
let combined_radius = circle_a.radius + circle_b.radius;
if ab.length_squared() < combined_radius * combined_radius {
let penetration_depth = combined_radius - ab.length();
let n = ab.normalize();
pos_a.0 -= n * penetration_depth * 0.5;
pos_b.0 += n * penetration_depth * 0.5;
}
}
}
In order to satisfy safety requirements, we need to make sure we don't mutate or access the same component twice, hence we add a check to make sure we don't operate on components from the same entity. It doesn't make much sense to check for collision against the same object anyway, so this makes perfect sense. Also, we make it a <= check, so we don't handle each pair twice.
Inside the loop we first need to check whether the objects overlap. We do that by checking the length of the vector from body a to body b.
let ab = pos_b.0 - pos_a.0;
if ab.length() < circle_a.radius + circle_b.radius {
todo!("Move circles to valid positions")
}
Actually, since we're comparing lengths of vectors, it's more efficient to compare square lengths, since that avoids the square root operation inside Vec2::length. So let's do that instead:
let ab = pos_b.0 - pos_a.0;
let combined_radius = circle_a.radius + circle_b.radius;
if ab.length_squared() < combined_radius * combined_radius {
todo!("Move circles to valid positions")
}
If you run the example now, the application should panic once the circles touch. Our collision check is working!
The next step is to actually resolve the collision. We do this by moving the circles away from each other, just enough so that they don't overlap. Our ab vector points from the first center to the second, so we can move each circle half of the penetration depth along this vector to make sure they don't touch anymore.
if ab.length_squared() < combined_radius * combined_radius {
let penetration_depth = combined_radius - ab.length();
let n = ab.normalize();
pos_a.0 -= n * penetration_depth * 0.5;
pos_b.0 += n * penetration_depth * 0.5;
}
If you run the simulation now, The two circles should move towards one another, then stop abruptly. We're finally seeing some interactions between objects!
Now you would probably expect two colliding balls to move away from each other after a collision occurs. At least if you imagined them as being somewhat bouncy. This bounciness is known as restitution in physics. Right now, all our collisions will behave as they had a coefficient of restitution of 0. We'll get back to that part later when we implement the SolveVelocities step.
For now we got a little bit more work to do in the position solver.
If we look at the code, there are some costly vector operations in there, that is: normalize() and length() . These both involve the same square root of a value we've already computed, so make sure we only do it once:
let ab_sqr_len = ab.length_squared();
if ab_sqr_len < combined_radius * combined_radius {
let ab_length = ab_sqr_len.sqrt();
let penetration_depth = combined_radius - ab_length;
let n = ab / ab_length;
pos_a.0 -= n * penetration_depth * 0.5;
pos_b.0 += n * penetration_depth * 0.5;
}
Second, there is the question of what happens if one circle is heavier than the other. In fact, let's copy our particle_collision.rs to a new example different_masses.rs.
And then make sure to override the masses. We'll set one particle to be three times heavier than the other.
// Left particle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert_bundle(ParticleBundle::new_with_pos_and_vel(
Vec2::new(-2., 0.),
Vec2::new(2., 0.),
))
.insert(Mass(3.)); // <-- new
// Right particle
commands
.spawn_bundle(PbrBundle {
mesh: sphere.clone(),
material: white.clone(),
..Default::default()
})
.insert_bundle(ParticleBundle::new_with_pos_and_vel(
Vec2::new(2., 0.),
Vec2::new(-2., 0.),
))
.insert(Mass(1.)); // <-- new
Now for this to make sense, the left sphere should affect the right circle more than the right circle affects the right, right? We still need to move the circles a total of penetration_depth away from each other, but it should be scaled proportionally to the masses of the circles.
It turns out that how much an object should be affected by a collision is proportional to its inverse mass and since the contributions from each particle should add up to 1 we get:
$$ w_i = \frac{1}{m_i} $$
$$ \Delta x_1 = -\frac{w_1}{w_1+w_2} d\vec{n} $$
$$ \Delta x_2 = \frac{w_2}{w_1+w_2} d\vec{n} $$
Translating to code, we get:
let ab_length = ab_sqr_len.sqrt();
let penetration_depth = combined_radius - ab_length;
let n = ab / ab_length;
let w_a = 1. / mass_a.0;
let w_b = 1. / mass_b.0;
let w_sum = w_a + w_b;
pos_a.0 -= n * penetration_depth * w_a / w_sum;
pos_b.0 += n * penetration_depth * w_b / w_sum;
If you run the example now, you should see that after the circles collide, they continue moving to the right. This is because as the left circle is corrected less than the right, it keeps some of its velocity.
Ok, we're done with position constraints for now. What we've implemented is known as a hard non-penetration constraint. We'll get back to soft constraints later, but for now, this this is all we need.
Solving velocities and adding bounce (restitution)
It's time to add some bounce to our collisions! This will be implemented in the SolveVelocities step.
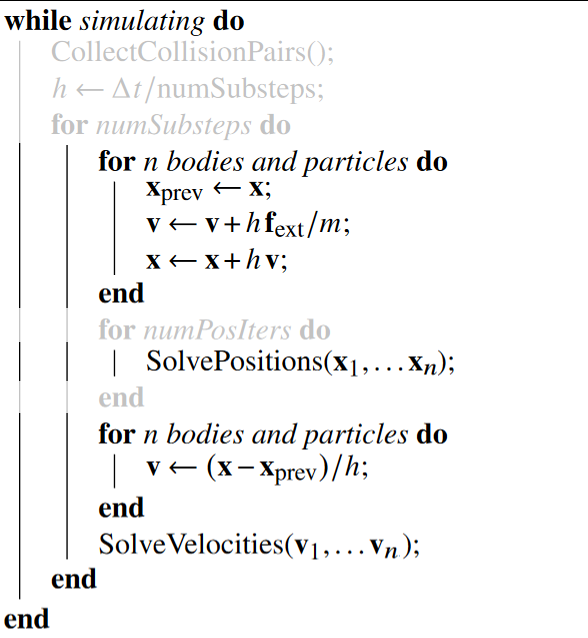
The notation from the XPBD paper is a bit deceptive. It looks as if SolveVelocities operates on the updated velocities form two lines above, but in fact, it needs both the updated, and the original predicted velocity in order to handle restitution (bounciness) and friction correctly.
So in order for this to work correctly we need to make sure the solve_vel system has access to the predicted and updated velocities. The updated velocities are already stored in the Vel components, but we also need to make sure we save the values someplace else as we predict them.
Let's create and add a new component, PreSolveVel.
// components.rs
#[derive(Component, Debug, Default)]
pub struct PreSolveVel(pub(crate) Vec2);
// entity.rs
pub struct ParticleBundle {
pub pos: Pos,
pub prev_pos: PrevPos,
pub mass: Mass,
pub collider: CircleCollider,
pub vel: Vel,
pub pre_solve_vel: PreSolveVel, // <-- new
}
And then update it in the integrate system:
fn integrate(
mut query: Query<(&mut Pos, &mut PrevPos, &mut Vel, &mut PreSolveVel, &Mass)>, // <-- new
gravity: Res<Gravity>,
) {
for (mut pos, mut prev_pos, mut vel, mut pre_solve_vel, mass) in query.iter_mut() { // <-- new
prev_pos.0 = pos.0;
let gravitation_force = mass.0 * gravity.0;
let external_forces = gravitation_force;
vel.0 += DELTA_TIME * external_forces / mass.0;
pos.0 += DELTA_TIME * vel.0;
pre_solve_vel.0 = vel.0; // <-- new
}
}
Another thing we're going to need, is to know what bodies actually collided in the SolvePositions step, so that we only solve velocities for pairs of bodies that actually collided.
You may be tempted to just copy the same loop we had in solve_pos , however, that will be pretty error prone, as the solve_pos corrections may move the bodies so that they no longer collide (even if you add a small collision margin).
So let's create a new resource to store the actual collisions, Contacts.
#[derive(Default, Debug)]
pub struct Contacts(pub Vec<(Entity, Entity)>);
And remember to initialize it:
app.init_resource::<Gravity>()
.init_resource::<Contacts>()
.add_stage_before(
Then update it in solve_pos, we now need to add Entity to the query as well:
fn solve_pos(
mut query: Query<(Entity, &mut Pos, &CircleCollider, &Mass)>,
mut contacts: ResMut<Contacts>,
) {
contacts.0.clear();
while let Some(
[(entity_a, mut pos_a, circle_a, mass_a), (entity_b, mut pos_b, circle_b, mass_b)],
) = iter.fetch_next()
{
// ...
if ab_sqr_len < combined_radius * combined_radius {
// ...
contacts.0.push((entity_a, entity_b)); // <-- new
}
Now that we have both velocities and the pairs of contacting bodies, we can start implementing solve_vel
We need to iterate over all pairs of colliding bodies, so let's create a loop that does just that:
fn solve_vel(
mut query: Query<(&mut Vel, &PreSolveVel, &Pos, &Mass)>,
contacts: Res<Contacts>,
) {
for (entity_a, entity_b) in contacts.0.iter().cloned() {
let (
(mut vel_a, pre_solve_vel_a, pos_a, circle_a, mass_a),
(mut vel_b, pre_solve_vel_b, pos_b, circle_b, mass_b),
) = unsafe {
// Ensure safety
assert!(entity_a != entity_b);
(
query.get_unchecked(entity_a).unwrap(),
query.get_unchecked(entity_b).unwrap(),
)
};
// TODO: make sure velocities are reflected and restitution/friction calculated
}
}
This is a bit ugly, but it it's what we need to do in order to get write access to two entities with the same types of components at once.
We need write access to Vel as well as read access to numerous other components.
Now, we're ready to start reflecting those momentums. When bouncy things collide, the momentum changes only in the direction of the collision normal.
If we consider the laws of preserving total momentum, we end up with the following:
fn solve_vel(mut query: Query<(&mut Vel, &PreSolveVel, &Pos, &Mass)>, contacts: Res<Contacts>) {
for (entity_a, entity_b) in contacts.0.iter().cloned() {
let (
(mut vel_a, pre_solve_vel_a, pos_a, mass_a),
(mut vel_b, pre_solve_vel_b, pos_b, mass_b),
) = unsafe {
// Ensure safety
assert!(entity_a != entity_b);
(
query.get_unchecked(entity_a).unwrap(),
query.get_unchecked(entity_b).unwrap(),
)
};
let n = (pos_b.0 - pos_a.0).normalize();
let pre_solve_relative_vel = pre_solve_vel_a.0 - pre_solve_vel_b.0;
let pre_solve_normal_vel = Vec2::dot(pre_solve_relative_vel, n);
let relative_vel = vel_a.0 - vel_b.0;
let normal_vel = Vec2::dot(relative_vel, n);
let restitution = 1.0;
let w_a = 1. / mass_a.0;
let w_b = 1. / mass_b.0;
let w_sum = w_a + w_b;
vel_a.0 += n * (-normal_vel - restitution * pre_solve_normal_vel) * w_a / w_sum;
vel_b.0 -= n * (-normal_vel - restitution * pre_solve_normal_vel) * w_b / w_sum;
}
}
Since we set restitution to 1, what we have here is a perfectly elastic collision. If you run the particle_collisions example you should now see that the particles are reflected with the same velocity they collide with. In the different_masses example one particle will be still, and the other will move fast off screen.
Now, it would be good if the coefficient of restitution was configurable, so we can represent different types of objects.
There doesn't seem to be a reasonable physical way to determine the restitution coefficient between two different materials. Wikipedia says it's commonly determined by experimentation. I did a quick review of some existing open-source engines, and to combine per-material coefficient in some way. Either by averaging or taking the minimum or maximum of the two coefficients.
Most physics engines seems to prefer averaging, so we will do that as well. We will add a Restitution component and add it to our circles:
// components.rs
#[derive(Component, Debug)]
pub struct Restitution(pub f32);
impl Default for Restitution {
fn default() -> Self {
Self(0.3)
}
}
// entity.rs
#[derive(Bundle, Default)]
pub struct ParticleBundle {
pos: Pos,
prev_pos: PrevPos,
mass: Mass,
collider: CircleCollider,
vel: Vel,
pre_solve_vel: PreSolveVel,
restitution: Restitution, // <-- new
}
Then update the solve_vel system to use the average of the two restitution values for the colliding circles:
fn solve_vel(
mut query: Query<(&mut Vel, &PreSolveVel, &Pos, &Mass, &Restitution)>,
contacts: Res<Contacts>,
) {
for (entity_a, entity_b) in contacts.0.iter().cloned() {
let (
(mut vel_a, pre_solve_vel_a, pos_a, mass_a, restitution_a),
(mut vel_b, pre_solve_vel_b, pos_b, mass_b, restitution_b),
) = unsafe {
// ...
let restitution = (restitution_a.0 + restitution_b.0) / 2.;
If you now run the example again, you should see that the particles are reflected, but now only keep 30% of their initial velocity.
You can play around with restitution in the examples if you like.
In the next part, we'll be making a more exiting example, and add some static boxes for our circles to collide with.