Physics engine - Part 3: Stacking and substepping

In this part, we'll continue implementing the XPBD algorithm. We'll start by looking at stacking, a common challenge in physics engines, and solve it by adding substepping.

XPBD again - adding substepping

We're going to finish another part of the XPBD algorithm, but before we start, let's create an example that helps motivate those parts. Create a new example ball_stacking.rs

use bevy::{
    diagnostic::{FrameTimeDiagnosticsPlugin, LogDiagnosticsPlugin},
    prelude::*,
};
use bevy_xpbd::*;

fn main() {
    App::new()
        .insert_resource(ClearColor(Color::rgb(0.8, 0.8, 0.9)))
        .insert_resource(Msaa { samples: 4 })
        .add_plugins(DefaultPlugins)
        .add_plugin(LogDiagnosticsPlugin::default())
        .add_plugin(FrameTimeDiagnosticsPlugin::default())
        .add_plugin(XPBDPlugin::default())
        .add_startup_system(spawn_camera)
        .add_startup_system(spawn_balls)
        .run();
}

fn spawn_camera(mut commands: Commands) {
    commands.spawn_bundle(OrthographicCameraBundle {
        transform: Transform::from_translation(Vec3::new(0., 0., 100.)),
        orthographic_projection: bevy::render::camera::OrthographicProjection {
            scale: 0.01,
            ..Default::default()
        },
        ..OrthographicCameraBundle::new_3d()
    });
}

fn spawn_balls(
    mut commands: Commands,
    mut materials: ResMut<Assets<StandardMaterial>>,
    mut meshes: ResMut<Assets<Mesh>>,
) {
    let sphere = meshes.add(Mesh::from(shape::Icosphere {
        radius: 1.,
        subdivisions: 4,
    }));

    let blue = materials.add(StandardMaterial {
        base_color: Color::rgb(0.4, 0.4, 0.6),
        unlit: true,
        ..Default::default()
    });

    let size = Vec2::new(20., 2.);
    commands
        .spawn_bundle(PbrBundle {
            mesh: meshes.add(Mesh::from(shape::Quad::new(Vec2::ONE))),
            material: blue.clone(),
            transform: Transform::from_scale(size.extend(1.)),
            ..Default::default()
        })
        .insert_bundle(StaticBoxBundle {
            pos: Pos(Vec2::new(0., -4.)),
            collider: BoxCollider { size },
            ..Default::default()
        });

    let radius = 0.15;
    let stacks = 5;
    for i in 0..15 {
        for j in 0..stacks {
            let pos = Vec2::new(
                (j as f32 - stacks as f32 / 2.) * 2.5 * radius,
                2. * radius * i as f32 - 2.,
            );
            let vel = Vec2::ZERO;
            commands
                .spawn_bundle(PbrBundle {
                    mesh: sphere.clone(),
                    material: blue.clone(),
                    transform: Transform {
                        scale: Vec3::splat(radius),
                        translation: pos.extend(0.),
                        ..Default::default()
                    },
                    ..Default::default()
                })
                .insert_bundle(ParticleBundle {
                    collider: CircleCollider { radius },
                    ..ParticleBundle::new_with_pos_and_vel(pos, vel)
                });
        }
    }
}

If you run it you will see one of the issues with our approach so far:

We got some stacks alright, but some of the balls are overlapping, and they appear squishy, not rigid.

The reason we get overlaps, is that our solver only solves position constraints one pair at a time, so some of the constraints are "fighting" each other. That is: a circle may be moved up by one constraint, then back down by another back into an overlapping position.

If we take another look at what we are missing from the XPBD algorithm:

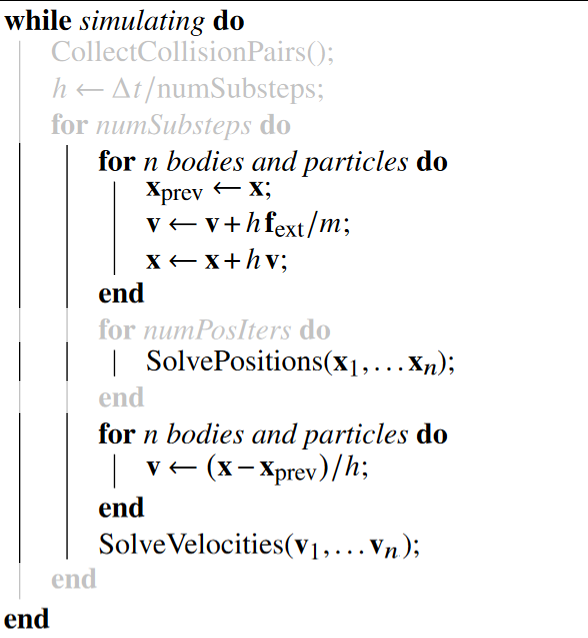
Time to look at those loops we've just ignored!

Let's look at the inner loop first, the one around SolvePositions . What this loop does is just run the position constraints multiple times, so the corrections have time to propagate and aren't "overwhelmed" by the gravity force. This is what's usually done in PBD-based physics simulations. According to the authors of the XPBD paper, however, it's significantly more effective to increase the number of substeps instead, so we will skip that innermost loop and remove it from the the algorithm:

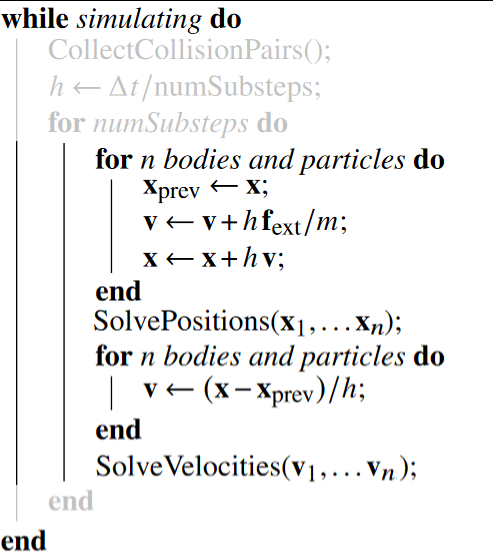
So now, the question is: What are substeps and how do we add them?

Sub-stepping simply divides up parts of the algorithm into smaller timesteps, by dividing DELTA_TIME by the number of substeps we want.

Actually, since we don't have CollectCollisionPairs yet and we've used DELTA_TIME all the placed XPBD uses h, we can actually just decrease the time step, and we will get the same effect.

So let's just divide our DELTA_TIME by the number of substeps we want:

pub const SUBSTEPS: i32 = 10;
pub const DELTA_TIME: f32 = 1. / 60. / SUBSTEPS as f32;

And with that... Our stacks look much nicer!

...but what happened to the frame rate? Depending on how powerful your machine is, the frame rate has dropped to a crawl (you can see the FPS logged in the console, on my laptop, I get around 3 FPS). If your machine is too beefy, you could simply increase the number of stacks to, say 40, and it should quickly drop.

So before we start looking into performance issues, we need to get some profiling data and make sure we're actually testing release builds. I like to use a tool called flamegraph. as it's pretty simple to set up and dead-simple to use.

cargo install flamegraph
cargo flamegraph --example ball_stacking

TODO: paste results

It's clear that we currently spending a lot of time in solve_pos. The reason it's so slow, is that we are checking collisions between every pair of spheres on our screen, since we have 15*20 = 300 balls, we've got 300 * 300 = 90,000 potential collisions.... And doing it over 10 times every single frame! No wonder my poor laptop is struggling.

So how do we deal with this?

One thing we could do, is of course to stop checking every possible pair, and instead only consider pairs that are somewhat close to each other. This process known as the collision broadphase, and is definitely worth doing. However, there is another thing we could do as well, and we'll start with that.

So this is where CollectCollisionPairs comes into play! The idea is that we only gather the list of potentially colliding bodies once per physics frame, and then repeat the sub-steps with the same list of potential collisions.

So lets look at how we can restructure our code to fit this approach and move our checks so they happen less often. First, revert the naive change that divided delta-time by sub-steps.

Then, we need some kind of data structure to store the "collision pairs". Once again, we will create a bevy resource, CollisionPairs, for this. Since we have quite a few resources already, let's move all of them to a new file, resources.rs

use bevy::prelude::*;

#[derive(Debug)]
pub struct Gravity(pub Vec2);

impl Default for Gravity {
    fn default() -> Self {
        Self(Vec2::new(0., -9.81))
    }
}

#[derive(Debug, Default)]
pub(crate) struct CollisionPairs(pub Vec<(Entity, Entity)>);

#[derive(Default, Debug)]
pub struct Contacts(pub Vec<(Entity, Entity, Vec2)>);

#[derive(Default, Debug)]
pub struct StaticContacts(pub Vec<(Entity, Entity, Vec2)>);

CollisionPairs is an implementation detail and so we give it crate visibility.

And add the module:

mod components;
mod entity;
mod resources;

pub use components::*;
pub use entity::*;
pub use resources::*;

And make sure to initialize the resource:

        app.init_resource::<Gravity>()
            .init_resource::<CollisionPairs>() // <-- new
            .init_resource::<Contacts>()
            .init_resource::<StaticContacts>()

So let's move our expensive collision checking out of solve_pos and over to our currently empty system: collect_collision_pairs.

fn collect_collision_pairs(
    query: Query<(Entity, &Pos, &CircleCollider)>,
    mut collision_pairs: ResMut<CollisionPairs>,
) {
    collision_pairs.0.clear();
    unsafe {
        for (entity_a, pos_a, circle_a) in query.iter_unsafe() {
            for (entity_b, pos_b, circle_b) in query.iter_unsafe() {
                // Ensure safety
                if entity_a <= entity_b {
                    continue;
                }

                let ab = pos_b.0 - pos_a.0;
                let combined_radius = circle_a.radius + circle_b.radius;

                let ab_sqr_len = ab.length_squared();
                if ab_sqr_len < combined_radius * combined_radius {
                    collision_pairs.0.push((entity_a, entity_b));
                }
            }
        }
    }
}

And only iterate over the collected pairs in solve_pos:

fn solve_pos(
    mut query: Query<(&mut Pos, &CircleCollider, &Mass)>,
    collision_pairs: Res<CollisionPairs>,
) {
    for (entity_a, entity_b) in collision_pairs.0.iter() {
        let (
            (mut pos_a, circle_a, mass_a),
            (mut pos_b, circle_b, mass_b),
        ) = unsafe {
            assert!(entity_a != entity_b); // Ensure we don't violate memory constraints
            (
                query.get_unchecked(*entity_a).unwrap(),
                query.get_unchecked(*entity_b).unwrap(),
            )
        };
        let ab = pos_b.0 - pos_a.0;
        let combined_radius = circle_a.radius + circle_b.radius;
        let ab_sqr_len = ab.length_squared();
        if ab_sqr_len < combined_radius * combined_radius {
            let ab_length = ab_sqr_len.sqrt();
            let penetration_depth = combined_radius - ab_length;
            let n = ab / ab_length;

            let w_a = 1. / mass_a.0;
            let w_b = 1. / mass_b.0;
            let w_sum = w_a + w_b;

            pos_a.0 -= n * penetration_depth * w_a / w_sum;
            pos_b.0 += n * penetration_depth * w_b / w_sum;
        }
}

If re-run the example, the performance hasn't gotten any better, we only moved the expensive code and we do the same amount of work. If we look at our flame graphs now, we will see that both solve_pos and solve_vel are nice and small-ish.

There is a problem with our code though. Did you spot it? Consider two circles that are almost touching. This pair would be discarded in collect_collision_pairs , but what happens if another constraints moves one of the circles so that they don't overlap anymore? Nothing. The circle's will happily overlap at the end of the physics frame, since it's not in the list of potential collision pairs, it's never corrected.

The XPBD authors recommend fixing this by introducing a safety margin when collecting the collision pairs.

fn collect_collision_pairs(
    query: Query<(Entity, &Pos, &Vel, &CircleCollider)>,
    mut collision_pairs: ResMut<CollisionPairs>,
) {
    collision_pairs.0.clear();

    let k = 2.; // safety margin multiplier bigger than 1 to account for sudden accelerations
    let safety_margin_factor = k * DELTA_TIME;
    let safety_margin_factor_sqr = safety_margin_factor * safety_margin_factor;

    unsafe {
        for (entity_a, pos_a, vel_a, circle_a) in query.iter_unsafe() {
            let vel_a_sqr = vel_a.0.length_squared();
            for (entity_b, pos_b, vel_b, circle_b) in query.iter_unsafe() {
                // Ensure safety
                if entity_a <= entity_b {
                    continue;
                }

                let ab = pos_b.0 - pos_a.0;
                let vel_b_sqr = vel_b.0.length_squared();
                let safety_margin_sqr = safety_margin_factor_sqr * (vel_a_sqr + vel_b_sqr);

                let combined_radius = circle_a.radius + circle_b.radius + safety_margin_sqr.sqrt();

                let ab_sqr_len = ab.length_squared();
                if ab_sqr_len < combined_radius * combined_radius {
                    collision_pairs.0.push((entity_a, entity_b));
                }
            }
        }
    }
}

Ok, now the fun part begins. Let's add the loop so we can run the solve steps many times per collect_collision_pairs.

First, we add a some new constants:

pub const DELTA_TIME: f32 = 1. / 60.;
pub const NUM_SUBSTEPS: u32 = 10;
pub const SUB_DT: f32 = DELTA_TIME / NUM_SUBSTEPS as f32;

Unfortunately, the rest isn't as fun as I'd like, but here it is anyway:

I haven't found a clean way to achieve nested repeated stages in bevy. You can repeat a whole stage by using run criteria that return ShouldRun::YesAndCheckAgain. In fact, this is what we already do with the FixedTimeStep run criteria. To add sub-stepping, we can replace that one with a more complex one that also tracks sub-stepping. In its essence, a run-criteria is a function that is called to check whether some part of the schedule should run or not. If we return YesAndCheckAgain the function will be called again after the part is finished, and we get a chance to run again. What we will do is actually keep CollectCollisionPairs and SyncTransforms inside the main loop, but we will only be executing them before/after the other systems on the first/last substep. So we add a variable tracking which substep we're on:

fn run_criteria(time: Res<Time>, mut state: ResMut<LoopState>) -> ShouldRun {
    if !state.has_added_time {
        state.has_added_time = true;
        state.accumulator += time.delta_seconds();
    }

    if state.substepping {
        state.current_substep += 1;

        if state.current_substep < NUM_SUBSTEPS {
            return ShouldRun::YesAndCheckAgain;
        } else {
            // We finished a whole step
            state.accumulator -= DELTA_TIME;
            state.current_substep = 0;
            state.substepping = false;
        }
    }

    if state.accumulator >= DELTA_TIME {
        state.substepping = true;
        state.current_substep = 0;
        ShouldRun::YesAndCheckAgain
    } else {
        state.has_added_time = false;
        ShouldRun::No
    }
}

And then run criteria for the before/after sub-stepping systems:

fn first_substep(state: Res<LoopState>) -> ShouldRun {
    if state.current_substep == 0 {
        ShouldRun::Yes
    } else {
        ShouldRun::No
    }
}

fn last_substep(state: Res<LoopState>) -> ShouldRun {
    if state.current_substep == NUM_SUBSTEPS - 1 {
        ShouldRun::Yes
    } else {
        ShouldRun::No
    }
}

Then we update our schedule with the new setup:

            .add_stage_before(
                CoreStage::Update,
                FixedUpdateStage,
                SystemStage::parallel()
                    .with_run_criteria(run_criteria) // <-- new
                    .with_system(
                        collect_collision_pairs
                            .with_run_criteria(first_substep) // <-- new
                            .label(Step::CollectCollisionPairs)
                            .before(Step::Integrate),
                    )
                    .with_system(integrate.label(Step::Integrate))
                    .with_system_set(
                        SystemSet::new()
                            .label(Step::SolvePositions)
                            .after(Step::Integrate)
                            .with_system(solve_pos)
                            .with_system(solve_pos_statics)
                            .with_system(solve_pos_static_boxes),
                    )
                    .with_system(
                        update_vel
                            .label(Step::UpdateVelocities)
                            .after(Step::SolvePositions),
                    )
                    .with_system_set(
                        SystemSet::new()
                            .label(Step::SolveVelocities)
                            .after(Step::UpdateVelocities)
                            .with_system(solve_vel)
                            .with_system(solve_vel_statics)
                            .with_system(solve_vel_static_boxes),
                    )
                    .with_system(
                        sync_transforms
                            .with_run_criteria(last_substep) // <-- new
                            .after(Step::SolveVelocities),
                    ),
            );

Now that we've added sub steps, we need to go through our code and look at all the places we previously used DELTA_TIME and replace it with SUB_DT in the places where things happen in the inner loop.

First, the systems:

fn integrate(
    mut query: Query<(&mut Pos, &mut PrevPos, &mut Vel, &mut PreSolveVel, &Mass)>,
    gravity: Res<Gravity>,
) {
    for (mut pos, mut prev_pos, mut vel, mut pre_solve_vel, mass) in query.iter_mut() {
        prev_pos.0 = pos.0;

        let gravitation_force = mass.0 * gravity.0;
        let external_forces = gravitation_force;
        vel.0 += SUB_DT * external_forces / mass.0;
        pos.0 += SUB_DT * vel.0;
        pre_solve_vel.0 = vel.0;
    }
}

// ...

fn update_vel(mut query: Query<(&Pos, &PrevPos, &mut Vel)>) {
    for (pos, prev_pos, mut vel) in query.iter_mut() {
        vel.0 = (pos.0 - prev_pos.0) / SUB_DT;
    }
}

And then we also need to update the bundle constructor in entity.rs since previous positions are now per sub step:

impl ParticleBundle {
    pub fn new_with_pos_and_vel(pos: Vec2, vel: Vec2) -> Self {
        Self {
            pos: Pos(pos),
            prev_pos: PrevPos(pos - vel * SUB_DT),
            vel: Vel(vel),
            ..Default::default()
        }
    }
}

And with that, we've implemented the full structure of the XPBD algorithm!

Now, if you run the example again, our stacks look nice and rigid with virtually no overlap.

And if you have a somewhat beefy computer, you should be able to get around 80 stacks with 10 substeps before performance starts to drop.

That concludes this tutorial. In the next one, we will add dynamic boxes and start worrying about rotation.