Physics engine - Part 5: Spinning and body builders
In this part, we'll add rotation to our dynamic and static rigid bodies + a short bonus section on body-builders.

There are two weird things still happening in our last example:
- The boxes are sliding along the ground without stopping
- The boxes don't tip over as their centers move past the corner of boxes below.
Adding orientation
Ok, we've put this off for far too long, it's finally time to make things spin!
The first thing we need is some way to represent a body's orientation. As we're doing this in 2D, a tempting option may be to use a simple f32 for counter-clockwise rotation angle in radians, i.e.:
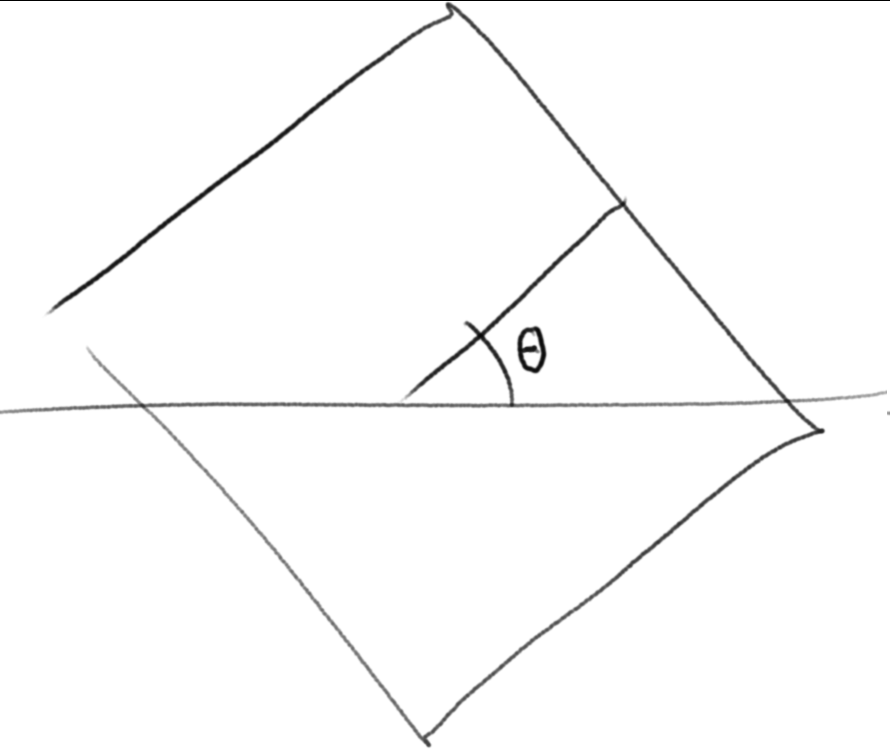
TODO: replace image
And certainly many 2D physics engines do exactly this. For instance Box2D and Chipmunk does it like this. However, there is one drawback, and that is that if we want to transform points (like a corner) from the local coordinate system of the box into world coordinates, we need to do the following:
$$ x_{world}=x_{center}+x_{local}\cos (\theta) - y_{local}\sin(\theta) $$
$$ y_{world}=y_{center}+y_{local}\cos (\theta) + x_{local}\sin(\theta) $$
I.e. we need two trigonometric functions. And we will need them a lot.
So instead, we opt for another approach, which is to store the sine and theta values instead of θ ****itself.
We can tell straight away that our new rotation component will need quite a few helpers and utility methods, so let’s make it a new module, rotation.rs :
use bevy::prelude::*;
#[derive(Debug, Clone, Copy, PartialEq)]
pub struct Rot {
cos: f32,
sin: f32,
}
And add it in lib.rs:
mod components;
mod contact;
mod entity;
mod resources;
mod utils;
mod rotation;
pub use components::*;
pub use entity::*;
pub use resources::*;
pub use rotation::*;
Let’s implement Default to be $\theta=0$.
impl Default for Rot {
fn default() -> Self {
Self::ZERO
}
}
impl Rot {
pub const ZERO: Self = Self { cos: 1., sin: 0. };
}
We can also add some convenience functions:
pub fn from_radians(radians: f32) -> Self {
Self {
cos: radians.cos(),
sin: radians.sin(),
}
}
pub fn from_degrees(degrees: f32) -> Self {
let radians = degrees.to_radians();
Self::from_radians(radians)
}
pub fn as_radians(&self) -> f32 {
f32::atan2(self.sin, self.cos)
}
Another thing we’re going to do a lot, is rotating vectors so let’s add a method for it:
pub fn rotate(&self, vec: Vec2) -> Vec2 {
Vec2::new(
vec.x * self.cos - vec.y * self.sin,
vec.x * self.sin + vec.y * self.cos,
)
}
It’s also interesting to be able to get the opposite rotation (i.e. to “subtract” angles), or do an inverse transformation if you think in terms of matrices. Since cos(-x) = cos(x) and sin(-x) = -sin(x), this simply becomes:
pub fn inv(self) -> Self {
Self {
cos: self.cos,
sin: -self.sin,
}
}
Going further along this route, let’s also add a way to combine two rotations, i.e. to add angles or multiply transformations. I’ve opted for the matrix terminology here:
pub fn mul(self, rhs: Rot) -> Self {
Self {
cos: self.cos * rhs.cos - self.sin * rhs.sin,
sin: self.sin * rhs.cos + self.cos * rhs.sin,
}
}
Now, let's add the new component to our bundles:
pub struct DynamicBoxBundle {
pub pos: Pos,
pub rot: Rot, // <-- here
pub prev_pos: PrevPos,
pub mass: Mass,
pub collider: BoxCollider,
pub vel: Vel,
pub pre_solve_vel: PreSolveVel,
pub restitution: Restitution,
pub aabb: Aabb,
}
// ...
pub struct DynamicBoxBundle {
pub pos: Pos,
pub rot: Rot, // <-- here
pub prev_pos: PrevPos,
pub mass: Mass,
pub collider: BoxCollider,
pub vel: Vel,
pub pre_solve_vel: PreSolveVel,
pub restitution: Restitution,
pub aabb: Aabb,
}
// ...
#[derive(Bundle, Default)]
pub struct StaticCircleBundle {
pub pos: Pos, // <-- here
pub rot: Rot,
pub collider: CircleCollider,
pub restitution: Restitution,
}
#[derive(Bundle, Default)]
pub struct StaticBoxBundle {
pub pos: Pos,
pub rot: Rot, // <-- here
pub collider: BoxCollider,
pub restitution: Restitution,
}
Let's add a simple example to play around with it, create a new file box_spin.rs:
use bevy::prelude::*;
use bevy_xpbd::*;
fn main() {
App::new()
.insert_resource(ClearColor(Color::BLACK))
.insert_resource(Msaa { samples: 4 })
.add_plugins(DefaultPlugins)
.add_plugin(XPBDPlugin::default())
.insert_resource(Gravity(Vec2::ZERO))
.add_startup_system(startup)
.run();
}
fn startup(
mut commands: Commands,
mut materials: ResMut<Assets<StandardMaterial>>,
mut meshes: ResMut<Assets<Mesh>>,
) {
let white = materials.add(StandardMaterial {
base_color: Color::WHITE,
unlit: true,
..Default::default()
});
commands
.spawn_bundle(PbrBundle {
mesh: meshes.add(Mesh::from(shape::Quad::new(Vec2::ONE))),
material: white.clone(),
..Default::default()
})
.insert_bundle(DynamicBoxBundle {
rot: Rot::from_degrees(45.),
..Default::default()
})
.insert(Mass(1.));
commands.spawn_bundle(OrthographicCameraBundle {
transform: Transform::from_translation(Vec3::new(0., 0., 100.)),
orthographic_projection: bevy::render::camera::OrthographicProjection {
scale: 0.01,
..Default::default()
},
..OrthographicCameraBundle::new_3d()
});
}
This should render a simple non-rotated box:

The box has a Rot component, but the visuals don't reflect it. Let's fix it by updating sync_transforms
/// Copies positions and rotations from the physics world to bevy Transforms
fn sync_transforms(mut query: Query<(&mut bevy::transform::components::Transform, &Pos, &Rot)>) {
for (mut transform, pos, rot) in query.iter_mut() {
transform.translation = pos.0.extend(0.);
transform.rotation = todo!("convert rot to a Quat");
}
}
So how do we do the conversion?
Well, the first thing we can do, is encapsulate the details of this in our Rot type by implementing From<Rot> for Quat:
impl From<Rot> for Quat {
fn from(_: Rot) -> Self {
todo!()
}
}
And call it in sync_transforms:
transform.rotation = (*rot).into();
Of course, we still need to implement it. We could just do:
Quat::from_rotation_z(rot.as_radians())
However, internally that calls atan2 first and then some sin and cos again, which is kind of unnecessary. If we look at how Quat::from_rotation_z is implemented, we find:
fn from_rotation_z(angle: T) -> Self {
let (s, c) = (angle * T::HALF).sin_cos();
Self::new(T::ZERO, T::ZERO, s, c)
}
If we copy this into our implementation, we get:
let angle = rot.as_radians();
let (s, c) = (angle * 0.5).sin_cos();
Quat::from_xyzw(0., 0., s, c)
And inlining as_radians:
let angle = f32::atan2(rot.sin, rot.cos);
let (s, c) = (angle * 0.5).sin_cos();
Quat::from_xyzw(0., 0., s, c)
We can see that what we have, is $\sin(\theta)$ and $\cos(\theta)$ and what we want is $\sin(\frac{\theta}{2})$ and $\cos(\frac{\theta}{2})$. If we use trigonometric identities, we arrive at the following:
$$ \sin(\frac{\theta}{2})=\sqrt{\frac{1-\cos(\theta)}{2}} $$
And for $\cos\frac\theta{2}$ we can do:
$$ \sin(2\theta)=2\sin\theta\cos\theta\ \sin\theta=2\sin\frac\theta2\cos\frac\theta2\ \cos\frac\theta2 = \frac{\sin\theta}{2\sin\frac\theta2} $$
We end up with:
impl From<Rot> for Quat {
fn from(rot: Rot) -> Self {
if rot.cos < 0. {
let t = 1. - rot.cos;
let d = 1. / (t * 2.).sqrt();
let z = t * d;
let w = -rot.sin * d;
Quat::from_xyzw(0., 0., z, w)
} else {
let t = 1. + rot.cos;
let d = 1. / (t * 2.).sqrt();
let z = -rot.sin * d;
let w = t * d;
Quat::from_xyzw(0., 0., z, w)
}
}
}
And now our square looks properly rotated:


So the floor is now tilted, but our physics systems don't yet know anything about rotation so let's fix that. We'll start with solve_pos_static_box_box which handles collisions between static boxes and the floor.
Adding in rotations to the queries, we get:
fn solve_pos_static_box_box(
mut dynamics: Query<(Entity, &mut Pos, &Rot, &BoxCollider), With<Mass>>,
statics: Query<(Entity, &Pos, &Rot, &BoxCollider), Without<Mass>>,
mut contacts: ResMut<StaticContacts>,
) {
for (entity_a, mut pos_a, rot_a, box_a) in dynamics.iter_mut() {
for (entity_b, pos_b, rot_b, box_b) in statics.iter() {
if let Some(Contact {
normal,
penetration,
}) = todo!()
{
constrain_body_position(&mut pos_a, normal, penetration);
contacts.0.push((entity_a, entity_b, normal));
}
}
}
}
So it's clear we need a new function in the contact module that handles contact between oriented boxes.
This is known as an obb-obb collision (oriented bounding box). There’s a pretty good explanation of how to do it on gamedev stackexchange, so I won’t go into details. Here’s the implementation I ended up with:
fn local_box_box(half_a: Vec2, ab: Vec2, rot_b: Rot, half_b: Vec2) -> Option<Contact> {
let v1 = rot_b.rotate(Vec2::new(half_b.x, half_b.y));
let v2 = rot_b.rotate(Vec2::new(half_b.x, -half_b.y));
let v3 = -v1;
let v4 = -v2;
let v1 = v1 + ab;
let v2 = v2 + ab;
let v3 = v3 + ab;
let v4 = v4 + ab;
let mut min_penetration = f32::MAX;
let mut n = Vec2::ZERO;
let v_max = v1.max(v2).max(v3.max(v4));
let v_min = v1.min(v2).min(v3.min(v4));
// right edge
{
let penetration = half_a.x - v_min.x;
if penetration < 0. {
return None;
} else if penetration < min_penetration {
min_penetration = penetration;
n = Vec2::X;
}
}
// left edge
{
let penetration = half_a.x + v_max.x;
if penetration < 0. {
return None;
} else if penetration < min_penetration {
min_penetration = penetration;
n = -Vec2::X;
}
}
// top edge
{
let penetration = half_a.y - v_min.y;
if penetration < 0. {
return None;
} else if penetration < min_penetration {
min_penetration = penetration;
n = Vec2::Y;
}
}
// bottom edge
{
let penetration = half_a.y + v_max.y;
if penetration < 0. {
return None;
} else if penetration < min_penetration {
min_penetration = penetration;
n = -Vec2::Y;
}
}
Some(Contact {
penetration: min_penetration,
normal: n,
})
}
pub fn box_box(
pos_a: Vec2,
rot_a: Rot,
size_a: Vec2,
pos_b: Vec2,
rot_b: Rot,
size_b: Vec2,
) -> Option<Contact> {
let half_a = size_a / 2.;
let half_b = size_b / 2.;
let ab = pos_b - pos_a;
let rot_ab = rot_a.inv().mul(rot_b);
if let Some(a_contact) = local_box_box(half_a, rot_a.inv().rotate(ab), rot_ab, half_b) {
// Check if there is a better separating axis along the other box' normals.
if let Some(b_contact) =
local_box_box(half_b, rot_b.inv().rotate(-ab), rot_ab.inv(), half_a)
{
if b_contact.penetration < a_contact.penetration {
return Some(Contact {
penetration: b_contact.penetration,
normal: rot_b.rotate(-b_contact.normal),
});
}
} else {
return None;
}
Some(Contact {
penetration: a_contact.penetration,
normal: rot_a.rotate(a_contact.normal),
})
} else {
None
}
}
And using it in the solve_pos systems:
fn solve_pos_static_boxes(
mut dynamics: Query<(Entity, &mut Pos, &CircleCollider), With<Mass>>,
statics: Query<(Entity, &Pos, &BoxCollider), Without<Mass>>,
mut contacts: ResMut<StaticContacts>,
) {
for (entity_a, mut pos_a, circle_a) in dynamics.iter_mut() {
for (entity_b, pos_b, box_b) in statics.iter() {
if let Some(Contact {
normal,
penetration,
}) = contact::ball_box(pos_a.0, circle_a.radius, pos_b.0, box_b.size)
{
constrain_body_position(&mut pos_a, normal, penetration);
contacts.0.push((entity_a, entity_b, normal));
}
}
}
}
fn solve_pos_static_box_box(
mut dynamics: Query<(Entity, &mut Pos, &Rot, &BoxCollider), With<Mass>>,
statics: Query<(Entity, &Pos, &Rot, &BoxCollider), Without<Mass>>,
mut contacts: ResMut<StaticContacts>,
) {
for (entity_a, mut pos_a, rot_a, box_a) in dynamics.iter_mut() {
for (entity_b, pos_b, rot_b, box_b) in statics.iter() {
if let Some(Contact {
normal,
penetration,
}) = contact::box_box(pos_a.0, *rot_a, box_a.size, pos_b.0, *rot_b, box_b.size)
{
constrain_body_position(&mut pos_a, normal, penetration);
contacts.0.push((entity_a, entity_b, normal));
}
}
}
}
And with that, the boxes should no longer be penetrating and should slide down along the slope:

It would be cool if the falling boxes were also rotated, so let's add that, following the pattern for pos and vel:
fn spawn_boxes(mut commands: Commands, materials: Res<Materials>) {
let size = Vec2::splat(0.3);
let pos = Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5) * 0.5 + Vec2::Y * 3.;
let vel = Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5);
let rot = random::<Rot>(); // <-- new
commands
.spawn_bundle(PbrBundle {
mesh: meshes.quad.clone(),
material: materials.blue.clone(),
transform: Transform {
scale: size.extend(1.),
translation: pos.extend(0.),
rotation: rot.into(), // <-- new
..Default::default()
},
..Default::default()
})
.insert_bundle(DynamicBoxBundle {
collider: BoxCollider { size },
rot, // <-- new
..DynamicBoxBundle::new_with_pos_and_vel(pos, vel)
});
}
Now, we will get some errors complaining because the Distribution<Rot> trait isn’t implemented for the Standard distribution type, which is necessary for using random(). So let's add that in rotation.rs:
impl Distribution<Rot> for Standard {
fn sample<R: rand::Rng + ?Sized>(&self, rng: &mut R) -> Rot {
let radians = rng.gen_range::<f32, _>(-PI..PI);
Rot::from_radians(radians)
}
}
And now we also need to move rand from dev-dependencies to the dependencies:
[dependencies]
bevy = "0.6"
rand = "0.8"
[dev-dependencies]
approx = "0.5"
We could, of course make it an optional dependency, and add a rand feature for our crate, but let’s keep it simple and add it when/if needed (yagni).
Okay, we're getting a bit off-topic, but now we having a way generate random rotations, which will come in handy later. Our example now compiles again:

Now, we do have rotated objects, and they collide with each other, but they're not really rotating. It gets clearer if we make the floor flat again:
rot: Rot::from_degrees(0.),

So obviously, we're going to need some kind of angular velocity. Before we go on, though: We've introduced a very subtle bug into our simulation. Did you spot it?
Once in a while, there is a very subtle "popping" behavior between two or more dynamic boxes. What's happening is that we haven't adjusted our aabb systems to account for rotation yet, so sometimes boxes that are penetrating, or will be penetrating during sub-stepping, are not properly added to CollisionPairs. When the bodies are penetrating even more, and are finally picked up by collect_collision_pairs they are corrected in solve_pos_static_boxes and are pushed all the way apart from each other in a single substep, and might even gain some extra velocity from it.
The reason it is working as well as it is, is because we expanded the Aabbs by COLLISION_PAIR_VEL_MARGIN_FACTOR * vel.length(). You can reduce that factor a bit, and you'll see the buggy behavior much clearer.
So let's fix update_aabb_box.
First, we'll update the query with the Rot component:
fn update_aabb_box(mut query: Query<(&mut Aabb, &Pos, &Rot, &Vel, &BoxCollider)>) {
for (mut aabb, pos, rot, vel, r#box) in query.iter_mut() {
Then, we'll use it to rotate the half extents. There is an excellent, though extremely brief answer on stackoverflow explaining this. Consider a rotated rectangle:
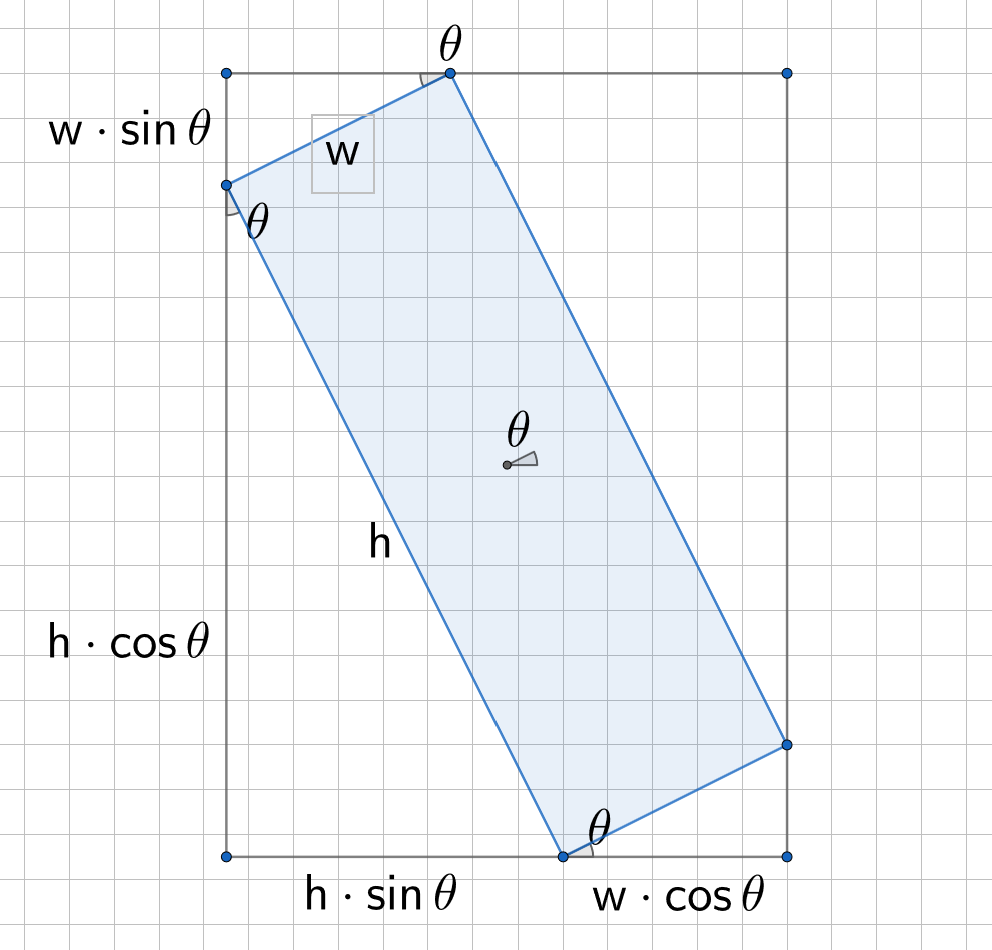
This figure holds for values of $\theta$ between 0 and $\frac\pi 2$. We see that the width of the AABB should be $h\sin\theta + w\cos\theta$, and similarly the height should be $h\cos\theta + w\sin\theta$.
In order handle other values of theta, we simply need to take the absolute value of those, so that gives us:
$$ w_{aabb} = h\lvert\sin\theta\rvert + w\lvert\cos\theta\rvert $$
$$ h_{aabb} = w\lvert\sin\theta\rvert + h\lvert\cos\theta\rvert $$
We already have $\sin\theta$ and $\cos\theta$ inside the rot component, so translating this to code, all we need to do is:
let sin = rot.sin().abs();
let cos = rot.cos().abs();
let box_w = r#box.size.x;
let box_h = r#box.size.y;
let w = box_h * sin + box_w * cos;
let h = box_w * sin + box_h * cos;
And then, as before, in order to get the min and max points, we need the half extents, so we divide by two and add the safety margin:
let margin = COLLISION_PAIR_VEL_MARGIN_FACTOR * vel.0.length();
let half_extents = Vec2::new(w / 2., h / 2.) + Vec2::splat(margin);
Rot::sin and Rot::cos are currently private fields, so we need to add accessors for them in rotation.rs:
impl Rot {
// ...
pub fn sin(self) -> f32 {
self.sin
}
pub fn cos(self) -> f32 {
self.cos
}
And finally, we have a (hopefully) bug-free simulation again!
Angular velocity
So getting back on track, we need our collisions to affect not only position, but also rotation. In order to get things spinning, we need to add another concept, angular velocity. We will handle it in much the same way we did regular velocities. That is, we'll add PrevRot, and AngVel components:
#[derive(Component, Debug, Default)]
pub struct PrevRot(pub Rot);
#[derive(Component, Debug, Default)]
pub struct AngVel(pub(crate) f32);
Note that the angular velocity is expressed as an angle (in radians per second), as using rotations for this would limit us to velocities in the -PI..PI radians-per-second range, as there is no way to distinguish between $\sin(\theta)$ and $\sin(2\pi{n} + \theta)$ and similarly for cosine.
And we add the new components to our bundle in entity.rs:
#[derive(Bundle, Default)]
pub struct DynamicBoxBundle {
pub pos: Pos,
pub rot: Rot,
pub prev_pos: PrevPos,
pub prev_rot: PrevRot,
pub mass: Mass,
pub collider: BoxCollider,
pub vel: Vel,
pub ang_vel: AngVel,
pub pre_solve_vel: PreSolveVel,
pub restitution: Restitution,
pub aabb: Aabb,
}
And finally, we'll add a new system for integrating rotations, basing it off the positional version, integrate, and ignoring external torque for now:
fn integrate_rot(mut query: Query<(&mut Rot, &mut PrevRot)>) {
for (mut rot, mut prev_rot) in query.iter_mut() {
prev_rot.0 = *rot;
rot += SUB_DT * ang_vel.0;
}
}
And add it to our schedule. Let's combine it in a system set together with integrate:
.with_system_set(
SystemSet::new()
.label(Step::Integrate)
.with_system(integrate)
.with_system(integrate_rot),
)
That way we will be running positional and rotational integration in parallel.
Okay, so we need some way to test if this integration step is doing what it should. Let's go ahead and add some initial angular velocity to the box_pour example:
First, we need a new bundle constructor:
impl DynamicBoxBundle {
pub fn new_with_pos_and_vel_and_rot_and_ang_vel(
pos: Vec2,
vel: Vec2,
rot: Rot,
ang_vel: f32,
) -> Self {
Self {
rot,
prev_rot: PrevRot(rot.mul(Rot::from_radians(-ang_vel * SUB_DT))),
ang_vel: AngVel(ang_vel),
..Self::new_with_pos_and_vel(pos, vel)
}
}
}
That's quite a mouthful. It's clear that our approach doesn't scale well with the number of components in each bundle. We'll look into that eventually, but for now we got quite a few things happening at once, so we'll stick with the simple stupid approach for now.
Finally, use the new constructor to add a bit of angular velocity in box_pour.rs:
fn spawn_boxes(mut commands: Commands, materials: Res<Materials>, meshes: ResMut<Meshes>) {
let size = Vec2::splat(0.3);
let pos = Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5) * 0.5 + Vec2::Y * 3.;
let vel = Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5);
let rot = random::<Rot>();
let ang_vel = random::<f32>() * 2. - 1.;
commands
.spawn_bundle(PbrBundle {
mesh: meshes.quad.clone(),
material: materials.blue.clone(),
transform: Transform {
scale: size.extend(1.),
translation: pos.extend(0.),
rotation: rot.into(),
..Default::default()
},
..Default::default()
})
.insert_bundle(DynamicBoxBundle {
collider: BoxCollider { size },
..DynamicBoxBundle::new_with_pos_and_vel_and_rot_and_ang_vel(pos, vel, rot, ang_vel)
});
}
And with that, our boxes should be constantly spinning, sliding along the floor. One step closer.
Rotation aware position solvers
The next thing we want to do, is actually change those velocities. Once again, we will be doing it in the same way as with position, so we need to implement update_ang_vel, basing it off update_vel, which will compute updated angular velocities based on how much the rotation has changed in the SolvePositions step:
fn update_ang_vel(mut query: Query<(&Rot, &PrevRot, &mut AngVel)>) {
for (rot, prev_rot, mut ang_vel) in query.iter_mut() {
ang_vel.0 = (prev_rot.0.inv().mul(*rot)).as_radians() / SUB_DT;
}
}
And add update the schedule with a new UpdateVelocities system set consisting of both update_vel and update_ang_vel:
.with_system_set(
SystemSet::new()
.label(Step::UpdateVelocities)
.after(Step::SolvePositions)
.with_system(update_vel)
.with_system(update_ang_vel)
)
And now, we're finally ready to start incorporating velocities into our solve systems.
Let's take a fresh look at what the non-penetration constraints are trying to prevent.
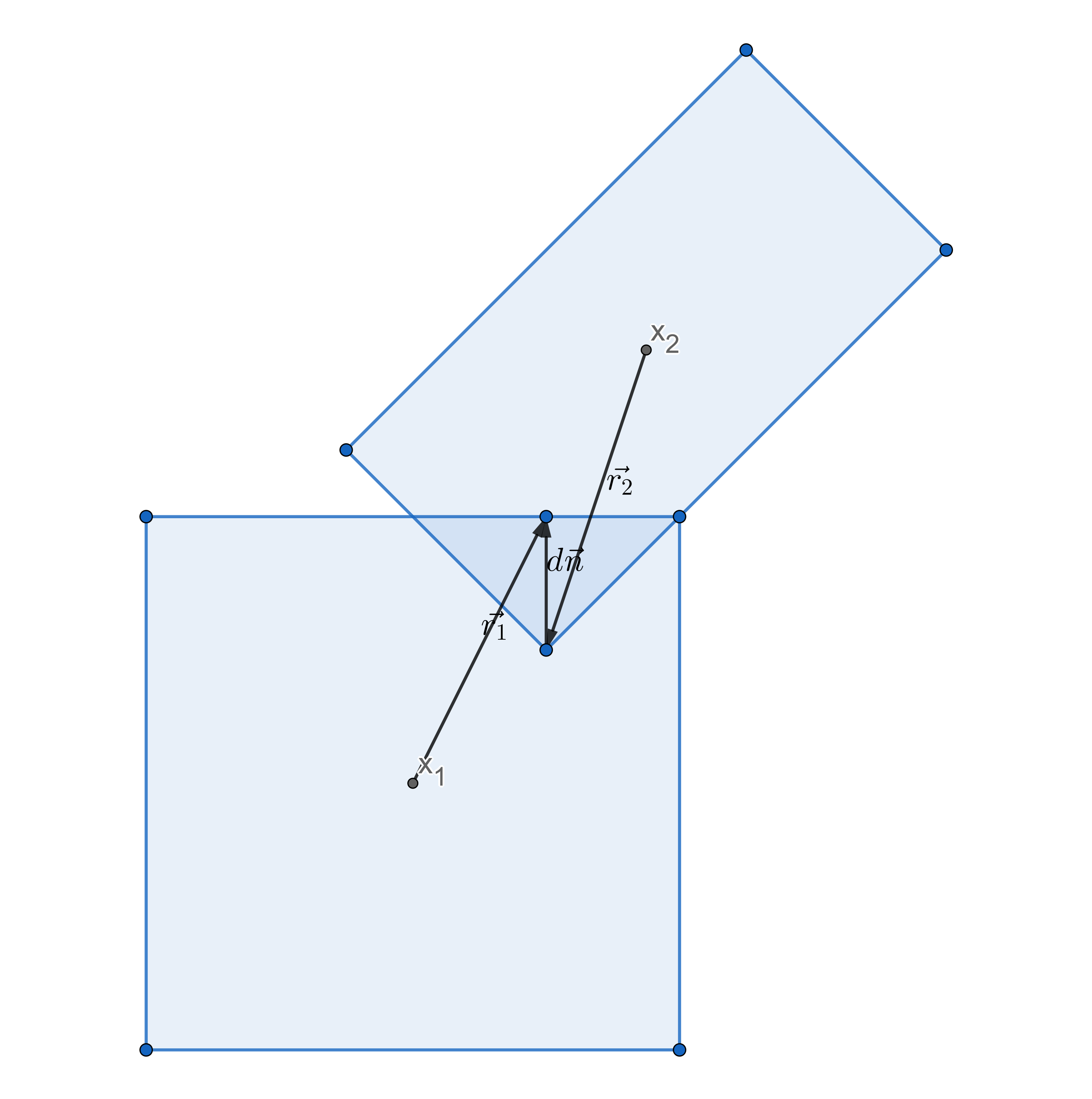
Currently, we're solving it by just pushing the object center positions, x₁ and x₂, d units away from each other along the normal, n.
If we add rotation into the mix, we can intuitively understand that we shouldn't move the center the entire $d\vec n$ of the way, as some of it should result in rotations of the boxes. What we really are trying to do, is move the two points, $\vec r_1$ and $\vec r_2$ so that the two shapes don't overlap anymore.
We should apply an impulse at $\vec{x_1}+\vec{r_1}$ instead
$$ \vec p = m \Delta \vec v_{cm} \
\vec r_\perp \cdot \vec p = I \Delta \omega $$
The velocity at the contact point is:
$$ \vec v = \vec v_{cm} + \omega \vec r_\perp $$
$$ \Delta v = [\Delta \vec v_{cm} + \Delta \omega \vec r_\perp] \cdot \vec n $$
Substituting $\Delta \vec v_{cm}$ and $\Delta \omega$
$$ \Delta v = [\vec pm^{-1} + (\vec r_\perp \cdot \vec p) I^{-1} \vec r_\perp] \cdot \vec n $$
Factoring out p ($\vec p = p \cdot \vec n$)
$$ \Delta v = p[\vec nm^{-1} + (\vec r_\perp \cdot \vec n) I^{-1} \vec r_\perp] \cdot \vec n $$
Expanding:
$$ \Delta v = p[\vec n \cdot \vec n m^{-1} + (\vec r_\perp \cdot \vec n) I^{-1} \vec r_\perp \cdot \vec n] $$
$$ \Delta v = p[m^{-1} + I^{-1}(\vec r_\perp \cdot \vec n) \vec r_\perp \cdot \vec n] $$
$$ \Delta v = p[m^{-1} + I^{-1}(\vec r_\perp \cdot \vec n)^2] $$
$$ \Delta v = pw $$
Where $w$ is generalized inverse mass.
Applying and impulse p at the contact point yields a total velocity change of
$$ \Delta v = \Delta v_1 + \Delta v_2 = p(w_1 + w_2) $$
In other words, we can change the velocity at the contact point by applying an impulse
$$ p = \frac {\Delta v} { w_1 + w_2 } $$
Then center of mass and angular velocity should be updated as follows:
$$ \Delta \vec v_{cm} = \vec p m^{-1} $$
$$ \Delta \omega = I^{-1}(\vec r_\perp \cdot \vec p) $$
To go from velocity to positional correction, we multiply conceptually by time so we get:
$$ p = \frac {\Delta x}{w_1 + w_2} $$
$$ \Delta x = \vec p m^{-1} $$
$$ \Delta \theta = I^{-1} \vec r_\perp \cdot \vec p $$
Okay, that’s a lot of formulas... now what does it mean for our implementation? Well first of all, it means we should no longer distribute the impulse according to the inverse mass alone, but the new definitions of w:
$$ w = m^{-1} + I^{-1}(\vec r_\perp \cdot \vec n)^2 $$
Okay, so we already have $m$ and $\vec n$, but we need $I^{-1}$ and $\vec r_\perp$.
$I$ is the moment of inertia. Wikipedia has a nice list of formulas if you don’t want to derive this for yourself. For a rectangle, it’s:
$$ I = \frac 1 {12} m (h^2 + w^2) $$
Consequently:
$$ I^{-1} = \frac{12}{m(w^2+h^2)} $$
So it’s made up of values we already have, easy.
let mass_a_inv = 1. / mass_a.0;
let i_a_inv = 12. * mass_a_inv / box_a.size.length_squared();
Now comes the tricky part, $\vec r_\perp$. $\vec r$ is the vector from the center of the body to the contact point on the edge of the collider, and $\vec r_\perp$ is its 90 degree counter-clockwise rotation. So how do we get $\vec r$?
Yet again, we need to modify our collision functions, this time so that they also return contact points. We will add two new fields to Contact:
#[derive(Debug, PartialEq)]
pub struct Contact {
pub penetration: f32,
pub normal: Vec2,
pub r_a: Vec2,
pub r_b: Vec2,
}
So how do we get those contact points. We could go total NIH, and implement it ourselves, but at this time however, we’re going to cheat.
This tutorial is about xpbd, and box-box collision with contact points is probably covered in detail other places on the web. Instead, we will make use of the excellent parry2d crate which is a low-level collision library which does more or less exactly what we want. As much as I like re-implementing the wheel, I do have limits. If we want we can always go and replace it later.
First, add parry2d to cargo.toml :
[dependencies]
bevy = "0.6"
rand = "0.8"
parry2d = "0.8"
We will be replacing most of our contact::box_box function with a simple call to parry2d::query::contact. The parry contact function takes the same conceptual inputs as our box_box function, all we have to do is convert to different types. Here is its declaration:
pub fn contact(
pos1: &Isometry<Real>,
g1: &dyn Shape,
pos2: &Isometry<Real>,
g2: &dyn Shape,
prediction: Real,
) -> Result<Option<Contact>, Unsupported> {
First we need to convert positions and rotations into the Isometry type. We’ll create a helper for this in contact.rs:
fn make_isometry(rotation: Rot, translation: Vec2) -> parry2d::math::Isometry<f32> {
parry2d::math::Isometry::<f32> {
rotation: rotation.into(),
translation: translation.into(),
}
}
So actually, this won’t compile... yet. The translation.into() call requires the glam-convert013 feature of nalgebra (one of parry2d’s dependencies) to be enabled in order to convert to/from Vec2. Enable it in cargo.toml:
TODO: Make sure this actually works with bevy 0.6 and nalgebra 0.30
parry2d = "0.8"
nalgebra = { version = "0.30", features = ["convert-glam020"] }
Okay, so now lets use our new helper in box_box
let pos1 = make_isometry(rot_a, pos_a);
let pos2 = make_isometry(rot_b, pos_b);
Next comes the &dyn Shape parameters. We want to pass in the parry2d::shape::Cuboid which implements this trait.
let cuboid1 = Cuboid::new((size_a / 2.).into());
let cuboid2 = Cuboid::new((size_b / 2.).into());
We have to divide the size by 2, since Cuboid::new takes in the half_extents in stead of the dimensions.
The prediction parameter is simply a kind of “padding” around our shapes, the function will only return None if the shapes are more than prediction apart. We are really only concerned with boxes that are actually touching, so we set it to 0.
let contact = parry2d::query::contact::contact(&pos1, &cuboid1, &pos2, &cuboid2, 0.0).unwrap();
Okay, so parry2d’s contact gives us a Contact type which is quite similar to our Contact, but not exactly. Here is its definition:
pub struct Contact {
/// Position of the contact on the first object.
pub point1: Point<Real>,
/// Position of the contact on the second object.
pub point2: Point<Real>,
/// Contact normal, pointing towards the exterior of the first shape.
pub normal1: Unit<Vector<Real>>,
/// Contact normal, pointing towards the exterior of the second shape.
///
/// If these contact data are expressed in world-space, this normal is equal to `-normal1`.
pub normal2: Unit<Vector<Real>>,
/// Distance between the two contact points.
///
/// If this is negative, this contact represents a penetration.
pub dist: Real,
}
We have defined our normal as pointing from a to b, so we will use normal1 as our normal. It uses distance, which is the opposite of our penetration, so we can simply negate that value. As you recall, we defined r_1 and r_2 as being the vectors from the centers of the shapes to the contact points, but point1 and point2 are given in world-space coordinates, which means we need to subtract the object positions. That means we need the following to convert to our Contact type:
match contact {
Some(c) => {
if c.dist > 0. {
None
} else {
Some(Contact {
penetration: -c.dist,
r_a: Into::<Vec2>::into(c.point1) - pos_a,
r_b: Into::<Vec2>::into(c.point2) - pos_b,
normal: (*c.normal1).into(),
})
}
}
None => None,
}
The complete contact::box_box function:
pub fn box_box(
pos_a: Vec2,
rot_a: Rot,
size_a: Vec2,
pos_b: Vec2,
rot_b: Rot,
size_b: Vec2,
) -> Option<Contact> {
let pos1 = make_isometry(rot_a, pos_a);
let pos2 = make_isometry(rot_b, pos_b);
let cuboid1 = Cuboid::new((size_a / 2.).into());
let cuboid2 = Cuboid::new((size_b / 2.).into());
let contact = parry2d::query::contact::contact(&pos1, &cuboid1, &pos2, &cuboid2, 0.0).unwrap();
match contact {
Some(c) => {
if c.dist > 0. {
None
} else {
Some(Contact {
penetration: -c.dist,
r_a: Into::<Vec2>::into(c.point1) - pos_a,
r_b: Into::<Vec2>::into(c.point2) - pos_b,
normal: (*c.normal1).into(),
})
}
}
None => None,
}
}
Let’s finally return to our solve systems. We finally have the $\vec r_1$ and $\vec r_2$ vectors we needed, as well as $I^{-1}$.
Let’s look at the code we had again:
let w_a = 1. / mass_a.0;
let w_b = 1. / mass_b.0;
let w_sum = w_a + w_b;
let pos_impulse = n * (-penetration_depth / w_sum);
pos_a.0 += pos_impulse * w_a;
pos_b.0 -= pos_impulse * w_b;
contacts.0.push((entity_a, entity_b, normal));
First we update the w_a and w_b parts to also include the rotational part, $I^{-1}(\vec r_\perp \cdot \vec n)^2$
let mass_a_inv = 1. / mass_a.0;
let mass_b_inv = 1. / mass_b.0;
let inertia_a_inv = 12. * mass_a_inv / box_a.size.length_squared();
let inertia_b_inv = 12. * mass_b_inv / box_b.size.length_squared();
let w_a_rot = inertia_a_inv * r_a.perp_dot(normal).powi(2);
let w_b_rot = inertia_b_inv * r_b.perp_dot(normal).powi(2);
let w_a = mass_a_inv + w_a_rot;
let w_b = mass_b_inv + w_b_rot;
Then we calculate the impulse as before:
let w = w_a + w_b;
let pos_impulse = normal * (-penetration / w);
And the positional updates are also like before:
pos_a.0 += pos_impulse * mass_a_inv;
pos_b.0 -= pos_impulse * mass_b_inv;
And finally, we can also update the angles ($\Delta \theta = I^{-1} \vec r_\perp \cdot \vec p$):
*rot_a = rot_a.mul(Rot::from_radians(
inertia_a_inv * r_a.perp_dot(pos_impulse)
));
*rot_b = rot_b.mul(Rot::from_radians(
inertia_b_inv * r_b.perp_dot(-pos_impulse),
));
Remember multiplying two rotations is the same as combining their angles.
And that completes solve_pos_box_box :
fn solve_pos_box_box(
mut query: Query<(&mut Pos, &mut Rot, &BoxCollider, &Mass)>,
mut contacts: ResMut<Contacts>,
collision_pairs: Res<CollisionPairs>,
) {
for (entity_a, entity_b) in collision_pairs.0.iter().cloned() {
if let Ok(((mut pos_a, mut rot_a, box_a, mass_a), (mut pos_b, mut rot_b, box_b, mass_b))) =
query.get_pair_mut(entity_a, entity_b)
{
if let Some(Contact {
normal,
penetration,
r_a,
r_b,
}) = contact::box_box(pos_a.0, *rot_a, box_a.size, pos_b.0, *rot_b, box_b.size)
{
let mass_a_inv = 1. / mass_a.0;
let mass_b_inv = 1. / mass_b.0;
let inertia_a_inv = 12. * mass_a_inv / box_a.size.length_squared();
let inertia_b_inv = 12. * mass_b_inv / box_b.size.length_squared();
let w_a_rot = inertia_a_inv * r_a.perp_dot(normal).powi(2);
let w_b_rot = inertia_b_inv * r_b.perp_dot(normal).powi(2);
let w_a = mass_a_inv + w_a_rot;
let w_b = mass_b_inv + w_b_rot;
let w = w_a + w_b;
let pos_impulse = normal * (-penetration / w);
pos_a.0 += pos_impulse * w_a;
pos_b.0 -= pos_impulse * w_b;
*rot_a = rot_a.mul(Rot::from_radians(inertia_a_inv * r_a.perp_dot(pos_impulse)));
*rot_b = rot_b.mul(Rot::from_radians(
inertia_b_inv * r_b.perp_dot(-pos_impulse),
));
contacts.0.push((entity_a, entity_b, normal));
}
}
}
}
Let’s give solve_pos_static_box_box the same treatment. We simplify the same way as we did previously, letting static objects have infinite inertia and mass:
fn solve_pos_static_box_box(
mut dynamics: Query<(Entity, &mut Pos, &mut Rot, &BoxCollider, &Mass)>,
statics: Query<(Entity, &Pos, &Rot, &BoxCollider), Without<Mass>>,
mut contacts: ResMut<StaticContacts>,
) {
for (entity_a, mut pos_a, mut rot_a, box_a, mass_a) in dynamics.iter_mut() {
for (entity_b, pos_b, rot_b, box_b) in statics.iter() {
if let Some(Contact {
normal,
penetration,
r_a: r,
r_b: _,
}) = contact::box_box(pos_a.0, *rot_a, box_a.size, pos_b.0, *rot_b, box_b.size)
{
let mass_inv = 1. / mass_a.0;
let i_inv = 12. * mass_inv / box_a.size.length_squared();
let w_rot = i_inv * r.perp_dot(normal).powi(2);
let w = mass_inv + w_rot;
let p = -normal * penetration / w;
pos_a.0 += p * mass_inv;
*rot_a = rot_a.mul(Rot::from_radians(i_inv * r.perp_dot(p)));
contacts.0.push((entity_a, entity_b, normal));
}
}
}
}
Ok, now we just need to solve some build issues. We modified Contact, but we haven’t updated our ball_ball and ball_box code accordingly. Let’s just put in todo!s for now:
Some(Contact {
normal,
penetration,
r_a: todo!(),
r_b: todo!(),
})
And similarly in the solve_pos_* systems where we get compiler errors:
if let Some(Contact {
normal,
penetration,
r_a: _, // <-- ignore r_a and r_b for now
r_b: _,
}) = contact::ball_ball(pos_a.0, circle_a.radius, pos_b.0, circle_b.radius)
And with that, the code should compile and our boxes should rotate somewhat realistically whenever they hit the ground or collide with each other.

Rotation aware velocity solver
So one thing that’s happening now, that’s a bit weird, is that once the boxes hit the ground, they bounce right up again, spinning like crazy. This is because our velocity solve step, is still unaware of rotation, and only considers relative velocity at the objects’ centers, not at the contact points.
So instead of simply $\vec v_{rel} = \vec v_a - \vec v_b$, we now have:
$$ \vec v_{rel} = (\vec v_a + \vec \omega_a × \vec r_a) - (\vec v_b + \vec \omega_b × \vec r_b) $$
In 2D, this becomes, where $\omega$ is a scalar, this becomes:
$$ \vec v_{rel} = (\vec v_a + \omega_a \vec r_{a\perp})-(\vec v_b + \omega_b \vec r_{b\perp}) $$
And in code:
let contact_vel_a = vel_a.0 + ang_vel_a.0 * r_a.perp();
let contact_vel_b = vel_b.0 + ang_vel_b.0 * r_b.perp();
let relative_vel = contact_vel_a - contact_vel_b;
We also need to do this for the pre_solve_relative_vel:
let pre_solve_contact_vel_a = pre_solve_vel_a.0 + pre_solve_ang_vel_a.0 * r_a.perp();
let pre_solve_contact_vel_b = pre_solve_vel_b.0 + pre_solve_ang_vel_b.0 * r_b.perp();
let pre_solve_relative_vel = pre_solve_contact_vel_a - pre_solve_contact_vel_b;
The computation of the normal and tangent velocity, $v_n$ and $v_t$, as well as the velocity correction, $\Delta \vec v$, is still the same, but we need to adjust how we apply the correction to the bodies.
It’s very similar to what we just did for the positions. We just add rotational parts into the weighted average, $w$, so the correction is split between the two bodies’ velocities and their angular velocities:
let w_rot_a = i_inv_a * r_a.perp_dot(n).powi(2);
let w_rot_b = i_inv_b * r_b.perp_dot(n).powi(2);
let w_a = 1. / mass_a.0 + w_rot_a;
let w_b = 1. / mass_b.0 + w_rot_b;
let w_sum = w_a + w_b;
let restitution_velocity = (-restitution * pre_solve_normal_vel).min(0.);
let vel_impulse = n * ((-normal_vel + restitution_velocity) / w_sum);
vel_a.0 += vel_impulse / mass_a.0;
vel_b.0 -= vel_impulse / mass_b.0;
ang_vel_a.0 += i_inv_a * r_a.perp_dot(vel_impulse);
ang_vel_b.0 += i_inv_b * r_b.perp_dot(-vel_impulse);
Ok, so we’re accessing quite a few variables that we haven’t yet declared. Well start at the top and deal with the compiler errors one by one. First, we have the pre_solve_ang_vel, this is analogous to pre_solve_vel, and we’ll deal with the exact same way:
Declare a struct in component.rs:
#[derive(Component, Debug, Default)]
pub struct PreSolveAngVel(pub(crate) f32);
Add it to the bundles in entity.rs:
pub pre_solve_ang_vel: PreSolveAngVel,
Update it in integrate_rot:
fn integrate_rot(mut query: Query<(&mut Rot, &mut PrevRot, &AngVel, &mut PreSolveAngVel)>) {
for (mut rot, mut prev_rot, ang_vel, mut pre_solve_ang_vel) in query.iter_mut() {
prev_rot.0 = *rot;
*rot = rot.mul(Rot::from_radians(SUB_DT * ang_vel.0));
pre_solve_ang_vel.0 = ang_vel.0;
}
}
And add it to our query in solve_vel:
fn solve_vel(
mut query: Query<(&mut Vel, &PreSolveVel, &PreSolveAngVel, &Mass, &Restitution)>,
contacts: Res<Contacts>,
) {
for (entity_a, entity_b, n) in contacts.0.iter().cloned() {
let (
(mut vel_a, pre_solve_vel_a, pre_solve_ang_vel_a, mass_a, restitution_a),
(mut vel_b, pre_solve_vel_b, pre_solve_ang_vel_b, mass_b, restitution_b),
) = query.get_pair_mut(entity_a, entity_b).unwrap();
Next up, we have r_a and r_b. We had these available in the solve_pos* systems, so let’s just add them to the Contacts resource.
#[derive(Default, Debug)]
pub struct Contacts(pub Vec<(Entity, Entity, Vec2, Vec2, Vec2)>);
So, this is getting quite messy, it’s hard to tell what’s what in that 5-tuple, so let’s go ahead and refactor it into a struct right away. We’ll name it BodyContact to avoid confusion with the existing Contact struct in the contact module.
#[derive(Debug, Clone)]
pub struct BodyContact {
pub entity_a: Entity,
pub entity_b: Entity,
pub r_a: Vec2,
pub r_b: Vec2,
pub normal: Vec2,
}
#[derive(Default, Debug)]
pub struct Contacts(pub Vec<BodyContact>);
And update solve_pos and solve_pos_box_box's contact.0.push() calls to fill the new struct:
contacts.0.push(BodyContact {
entity_a,
entity_b,
r_a,
r_b,
normal,
});
And use it in solve_vel:
for BodyContact {
entity_a,
entity_b,
r_a,
r_b,
normal: n,
} in contacts.0.iter().cloned()
Phew, finally we have r_a and r_b.
Next up is ang_vel_a and ang_vel_b. We simply add them to the query:
mut query: Query<(
&mut Vel,
&mut AngVel,
&PreSolveVel,
&PreSolveAngVel,
&Mass,
&Restitution,
)>,
// ...
let (
(mut vel_a, mut ang_vel_a, pre_solve_vel_a, pre_solve_ang_vel_a, mass_a, restitution_a),
(mut vel_b, mut ang_vel_b, pre_solve_vel_b, pre_solve_ang_vel_b, mass_b, restitution_b),
) = query.get_pair_mut(entity_a, entity_b).unwrap();
And that leaves i_inv_a and i_inv_b. We’ve changed quite a few things already, so before we actually implement it, let’s just fake it. We know that our boxes are 0.3x0.3 units with mass 1, and that the formula for inverse box inertia is:
$$ I^{-1}_{box} = \frac{12} {m (w^2+h^2)} = \frac {12} {1 \cdot (0.3^2 + 0.3^2)} \approx 67 $$
So let’s just fake it for now:
let inertia_a_inv = 67.;
let inertia_b_inv = 67.;
And finally, our code should compile again. And we can once again enjoy the shower of cubes.

It should look a lot more realistic now, as the cubes “tip” over when they land on a corner.
Keeping it clean
Ok, so let’s go back and fix that ugly inertia hack.
We are computing inertia in the solve_pos* systems based on the collider and the mass, so we could just do the same in solve_vel. However that would drag in the BoxCollider into the query, and it would also be nice to be able to specify a custom inertia as some shapes don’t necessarily have mass distributed evenly across their surface area. I.e. bodies that have more of their mass gathered at the center will be easier to rotate.
Instead, we create a new Inertia component:
#[derive(Component, Debug, Default, Clone)]
pub struct Inertia {
pub inv: f32,
}
Instead of storing the actual inertia, we’ll store the inverse inertia because that’s what we usually use in computations.
And add it in entity.rs:
#[derive(Bundle, Default)]
pub struct DynamicBoxBundle {
pub pos: Pos,
pub rot: Rot,
pub prev_pos: PrevPos,
pub prev_rot: PrevRot,
pub mass: Mass,
pub inertia: Inertia, // <-- new
pub collider: BoxCollider,
pub vel: Vel,
pub ang_vel: AngVel,
pub pre_solve_vel: PreSolveVel,
pub pre_solve_ang_vel: PreSolveAngVel,
pub restitution: Restitution,
pub aabb: Aabb,
}
Now, we just need to compute it somewhere. Since the computation of inertia for uniformly distributed mass is shape dependent, we add it on the BoxCollider struct in components.rs:
impl BoxCollider {
pub fn inertia_inv_from_mass_inv(&self, mass_inv: f32) -> f32 {
12. * mass_inv / self.size.length_squared()
}
}
And now we can call it in box_pour.rs:
let collider = BoxCollider { size };
let mass = Mass(1.);
let inertia = Inertia {
inv: collider.inertia_inv_from_mass_inv(1. / mass.0),
};
commands
.spawn_bundle(PbrBundle {
mesh: meshes.quad.clone(),
material: materials.blue.clone(),
transform: Transform {
scale: size.extend(1.),
translation: pos.extend(0.),
rotation: rot.into(),
..Default::default()
},
..Default::default()
})
.insert_bundle(DynamicBoxBundle {
collider,
inertia,
mass,
..DynamicBoxBundle::new_with_pos_and_vel_and_rot_and_ang_vel(pos, vel, rot, ang_vel)
});
}
And finally, let’s use it in the solve_* systems:
fn solve_pos_box_box(
mut query: Query<(&mut Pos, &mut Rot, &BoxCollider, &Mass, &Inertia)>,
mut contacts: ResMut<Contacts>,
collision_pairs: Res<CollisionPairs>,
) {
for (entity_a, entity_b) in collision_pairs.0.iter().cloned() {
if let Ok((
(mut pos_a, mut rot_a, box_a, mass_a, inertia_a),
(mut pos_b, mut rot_b, box_b, mass_b, inertia_b),
// ...
let w_a_rot = inertia_a.inv * r_a.perp_dot(normal).powi(2);
let w_b_rot = inertia_b.inv * r_b.perp_dot(normal).powi(2);
// ...
*rot_a = rot_a.mul(Rot::from_radians(inertia_a.inv * r_a.perp_dot(pos_impulse)));
*rot_b = rot_b.mul(Rot::from_radians(
inertia_b.inv * r_b.perp_dot(-pos_impulse),
));
// ...
fn solve_pos_static_box_box(
mut dynamics: Query<(Entity, &mut Pos, &mut Rot, &BoxCollider, &Mass, &Inertia)>,
// ...
for (entity_a, mut pos_a, mut rot_a, box_a, mass_a, inertia_a) in dynamics.iter_mut() {
// ...
let w_rot = inertia_a.inv * r_a.perp_dot(normal).powi(2);
// ...
let delta_rot = inertia_a.inv * r_a.perp_dot(p);
fn solve_vel(
mut query: Query<(
&mut Vel,
&mut AngVel,
&PreSolveVel,
&PreSolveAngVel,
&Mass,
&Inertia,
&Restitution,
)>,
contacts: Res<Contacts>,
) {
// ...
let (
(
mut vel_a,
mut ang_vel_a,
pre_solve_vel_a,
pre_solve_ang_vel_a,
mass_a,
inertia_a,
restitution_a,
),
(
mut vel_b,
mut ang_vel_b,
pre_solve_vel_b,
pre_solve_ang_vel_b,
mass_b,
inertia_b,
restitution_b,
),
) = query.get_pair_mut(entity_a, entity_b).unwrap();
// ...
let w_rot_a = inertia_a.inv * r_a.perp_dot(n).powi(2);
let w_rot_b = inertia_b.inv * r_b.perp_dot(n).powi(2);
// ...
ang_vel_a.0 += inertia_a.inv * r_a.perp_dot(vel_impulse);
ang_vel_b.0 += inertia_b.inv * r_b.perp_dot(-vel_impulse);
// ...
fn solve_vel_statics(
mut dynamics: Query<(
&mut Vel,
&mut AngVel,
&PreSolveVel,
&PreSolveAngVel,
&Mass,
&Inertia,
&Restitution,
)>,
statics: Query<&Restitution, Without<Mass>>,
contacts: Res<StaticContacts>,
) {
// ...
let (
mut vel_a,
mut ang_vel_a,
pre_solve_vel_a,
pre_solve_ang_vel_a,
mass_a,
inertia_a,
restitution_a,
) = dynamics.get_mut(entity_a).unwrap();
// ...
let w_rot = inertia_a.inv * r_a.perp_dot(n).powi(2);
// ...
ang_vel_a.0 += inertia_a.inv * r_a.perp_dot(vel_impulse);
And finally everything should work again.

You can now play around with it by changing the inverse inertia of the boxes. If you set it to 0., rotation will be virtually “unchangeable” by the solve_* systems. and you would get the same behavior as before we started adding rotation aware solving.
Body builders
Another thing that’s pretty ugly, is the way we initialize bodies:
..DynamicBoxBundle::new_with_pos_and_vel_and_rot_and_ang_vel(pos, vel, rot, ang_vel)
And it’s up to the user to remember to add the correct Inertia for a given collider, which is also not exactly nice.
A common way to deal with this in rust, is using the builder pattern. It’s kind of weird to be using it here, since bevy’s spawn_bundle and .inserts are in a way a builder pattern itself, but the challenge here is that we have quite a few components that we’d like to default to being computed based on the value of other components, but still allow the user to override. For example, it would be nice if the mass defaulted to the area of the collider and inertia defaulted to a uniform distribution of mass in that collider.
We’ll use the derive_builder crate for this, as it lets us implement the builder pattern with amazingly little boilerplate
Add it as a dependency:
cargo add derive_builder
And add the following annotations to DynamicBoxBundle:
#[derive(Bundle, Default, Clone, Builder)]
#[builder(default)]
pub struct DynamicBoxBundle {
pub pos: Pos,
pub rot: Rot,
#[builder(setter(skip), default = "self.default_prev_pos()")]
pub prev_pos: PrevPos,
#[builder(setter(skip), default = "self.default_prev_rot()")]
pub prev_rot: PrevRot,
pub mass: Mass,
#[builder(default = "self.default_inertia()")]
pub inertia: Inertia,
pub collider: BoxCollider,
pub vel: Vel,
pub ang_vel: AngVel,
pub pre_solve_vel: PreSolveVel,
pub pre_solve_ang_vel: PreSolveAngVel,
pub restitution: Restitution,
pub aabb: Aabb,
}
impl DynamicBoxBundleBuilder {
fn default_prev_pos(&self) -> PrevPos {
let vel = self.vel.unwrap_or_default();
let pos = self.pos.unwrap_or_default();
PrevPos(pos.0 - vel.0 * SUB_DT)
}
fn default_prev_rot(&self) -> PrevRot {
let ang_vel = self.ang_vel.unwrap_or_default();
let rot = self.rot.unwrap_or_default();
PrevRot(rot.mul(Rot::from_radians(-ang_vel.0 * SUB_DT)))
}
fn default_inertia(&self) -> Inertia {
let mass = self.mass.unwrap_or_default();
let collider = self.collider.unwrap_or_default();
Inertia {
inv: collider.inertia_inv_from_mass_inv(1. / mass.0),
}
}
}
And this generates a DynamicBoxBundleBuilder implementation for us. Let’s make use of it in the box_pour example:
fn spawn_boxes(mut commands: Commands, materials: Res<Materials>) {
let size = Vec2::splat(0.3);
let pos = Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5) * 0.5 + Vec2::Y * 3.;
let rot = random::<Rot>();
commands
.spawn_bundle(PbrBundle {
mesh: meshes.quad.clone(),
material: materials.blue.clone(),
transform: Transform {
scale: size.extend(1.),
translation: pos.extend(0.),
rotation: rot.into(),
..Default::default()
},
..Default::default()
})
.insert_bundle(
DynamicBoxBundleBuilder::default()
.collider(BoxCollider { size })
.pos(Pos(pos))
.rot(rot)
.vel(Vel(Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5)))
.ang_vel(AngVel(random::<f32>() * 2. - 1.))
.build()
.unwrap(),
);
}
No more crazy long constructors, and we could also specify only ang_vel, without vel, if we wanted that.
There is one more thing we can do to make this nicer, though. Notice the repetition of the Pos and other newtypes everywhere:
.pos(Pos(pos))
It’s kind of redundant since we know that it’s a position, it would be more ergonomic to be able to just pass in aVec2 directly. We can enable this behavior by enabling the setter(into) for the builder:
use derive_builder::Builder;
// ...
#[derive(Bundle, Default, Clone, Builder)]
#[builder(default, setter(into))]
pub struct DynamicBoxBundle {
This makes the builder field setters generic over types that implement the Into trait, so if we simply implement From for our newtypes, this should work, i.e.:
impl From<Vec2> for Pos {
fn from(pos: Vec2) -> Self {
Pos(pos)
}
}
Now we can remove Pos and get rid of one level of redundancy:
.pos(pos)
Now, we could implement From for the other newtypes as well (BoxCollider, Vel, AngVel etc.), but that would be quite tedious, so instead we make use of another crate that cuts down on this boiler-plate as well, derive_more:
cargo add derive_more
And now we can remove the From<Vec2> for Pos implementation and simply derive it instead:
use derive_more::From;
// ...
#[derive(Debug, Default, Clone, Copy, From)]
pub struct Pos(pub Vec2);
Do the same thing for the other newtypes as well: PrevPos, Mass, Restitution, CircleCollider, BoxCollider, Vel, PreSolveVel, PrevRot, AngVel, PreSolveAngVel. I won’t post the code this time, I trust you’ll figure it out on your own.
Now, you can simplify the usage further:
DynamicBoxBundleBuilder::default()
.collider(size)
.pos(pos)
.rot(rot)
.vel(Vec2::new(random::<f32>() - 0.5, random::<f32>() - 0.5))
.ang_vel(random::<f32>() * 2. - 1.)
.build()
.unwrap(),
Let’s also implement a sensible default for the mass, based on the collider area:
#[builder(default = "self.default_mass()")]
pub mass: Mass,
// ...
fn default_mass(&self) -> Mass {
let collider = self.collider.unwrap_or_default();
(collider.size.x * collider.size.y).into()
}
Now, in order for the inertia to still be correct, we have to use our new method in case Mass hasn’t been specified (or we’d compute it based on the Mass::default() value of 1. instead):
fn default_inertia(&self) -> Inertia {
let mass = self.mass.unwrap_or_else(|| self.default_mass());
let collider = self.collider.unwrap_or_default();
Inertia {
inv: collider.inertia_inv_from_mass_inv(1. / mass.0),
}
}
Now, our boxes in box_pour should default to have a mass of 0.3 * 0.3 = 0.09 instead of 1.. And inertia should be set accordingly. Of course, everything will still behave the same because all our boxes have the same size, so mass is kind of irrelevant in this particular example.
Now, the usage of DynamicBoxBundle, is starting to get pretty ergonomic. There is still more work to be done here, for instance we still have the exact same problem with the ParticleBundle, and in fact we’ve completely neglected it since we started working with boxes. We will get back to it soon, but I don’t want go too far off-topic with refactoring. Instead we'll finish our discussion on solving rotations before we get back to the balls.